Hypothesis tests

# Hypothesis testing

**Session 2**

]

---

# Outline
--

.box-2.medium.sp-after-half[Variability]

.box-4.medium.sp-after-half[Hypothesis tests]

.box-5.medium.sp-after-half[Pairwise comparisons]

---

layout: false
name: signal-vs-noise
class: center middle section-title section-title-2 animated fadeIn

# Sampling variability

---

---

# Studying a population
.medium[

Interested in impacts of intervention or policy

]

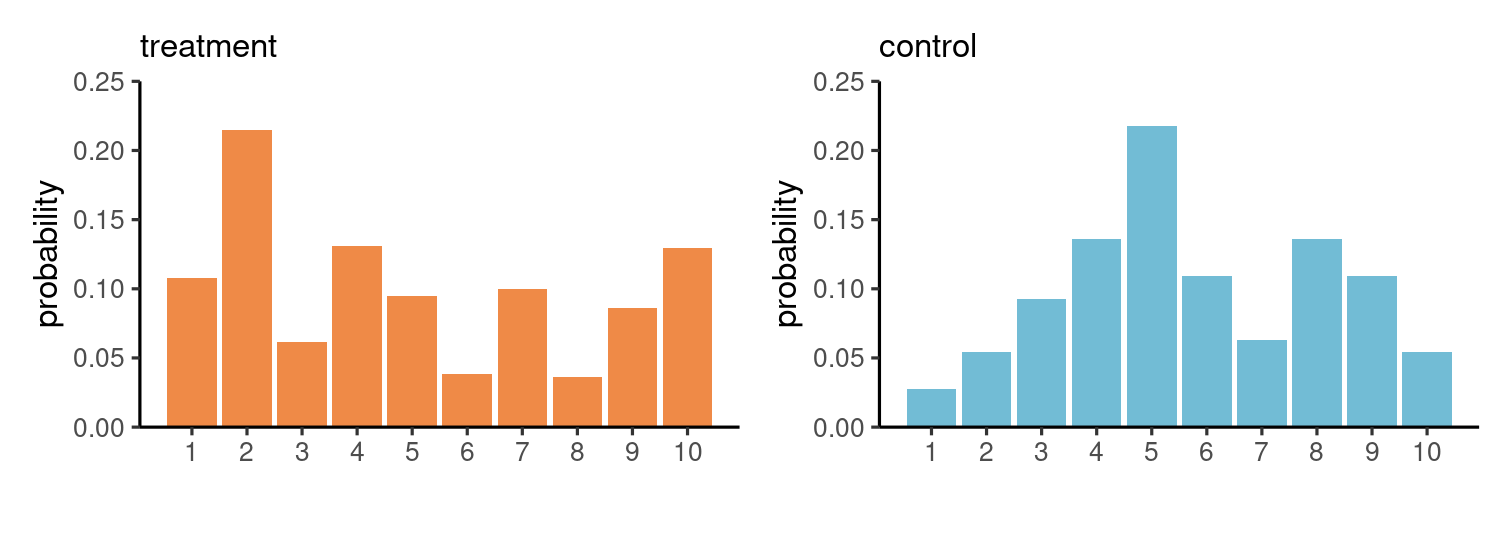
Population distribution (describing possible outcomes and their frequencies) encodes everything we could be interested in.

---

# Sampling variability

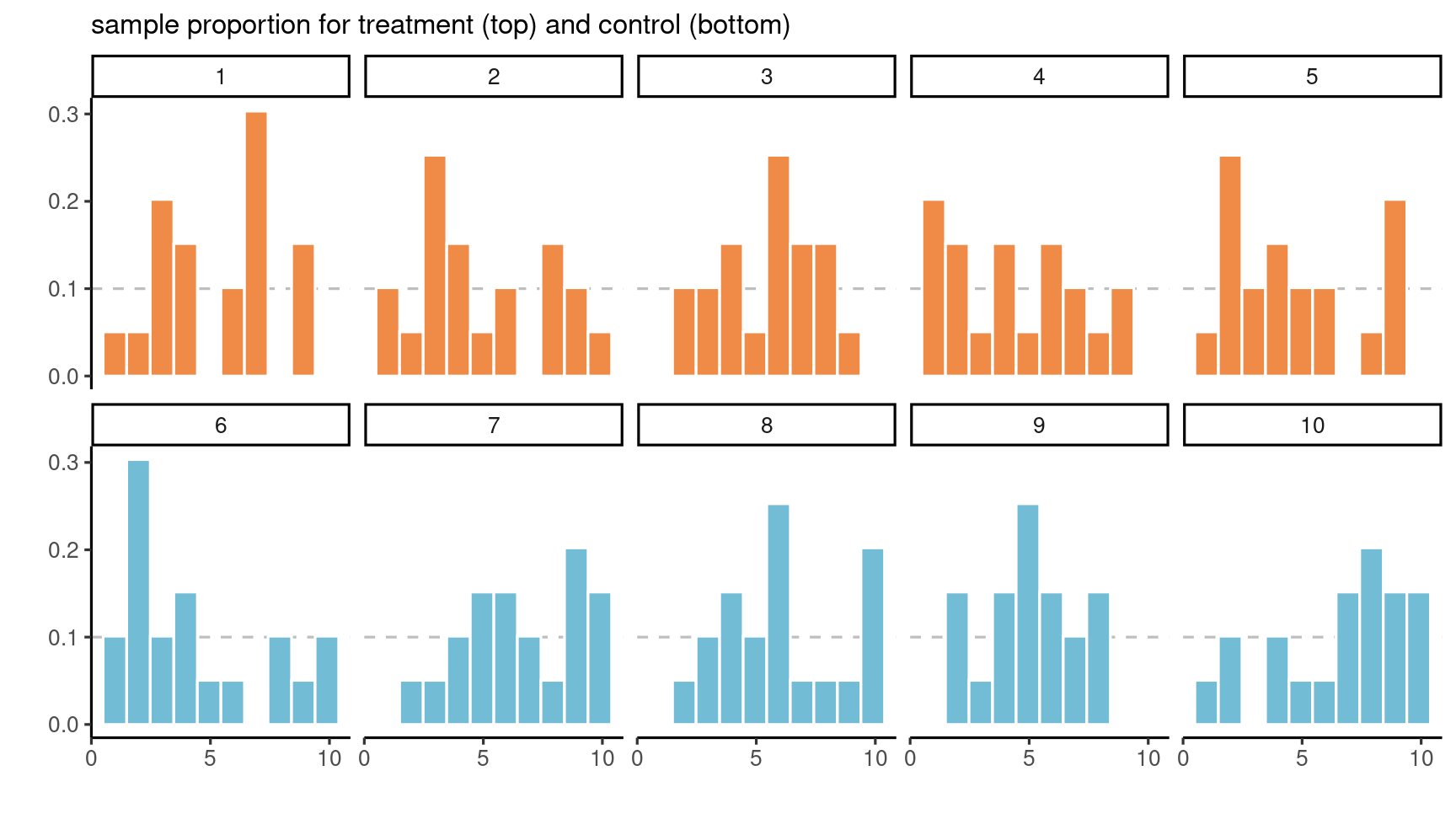
<img src="02-slides_files/figure-html/unifsamp1-1.png" width="80%" style="display: block; margin: auto;" />
.tiny[

Histograms for 10 random samples of size 20 from a discrete uniform distribution.

]

---

# Decision making under uncertainty

`$\to$` limited information available about population.
   
- Sample too small to reliably estimate distribution   
   
- Focus instead on particular summaries
  
  `$\to$` mean, variance, odds, etc.

]

---

# Population characteristics

`$$\mu$$`

.box-inv-2.medium.sp-after-half[
standard deviation
]

`$$\sigma= \sqrt{\text{variance}}$$`
.center[
same scale as observations
]

]

]

???

Do not confuse standard error (variability of statistic) and standard deviation (variability of observation from population)

---

# Sampling variability

???

Not all samples are born alike
- Analogy: comparing kids (or siblings): not everyone look alike (except twins...)
- Chance and haphazard variability mean that we might have a good idea, but not exactly know the truth.

---

# The signal and the noise

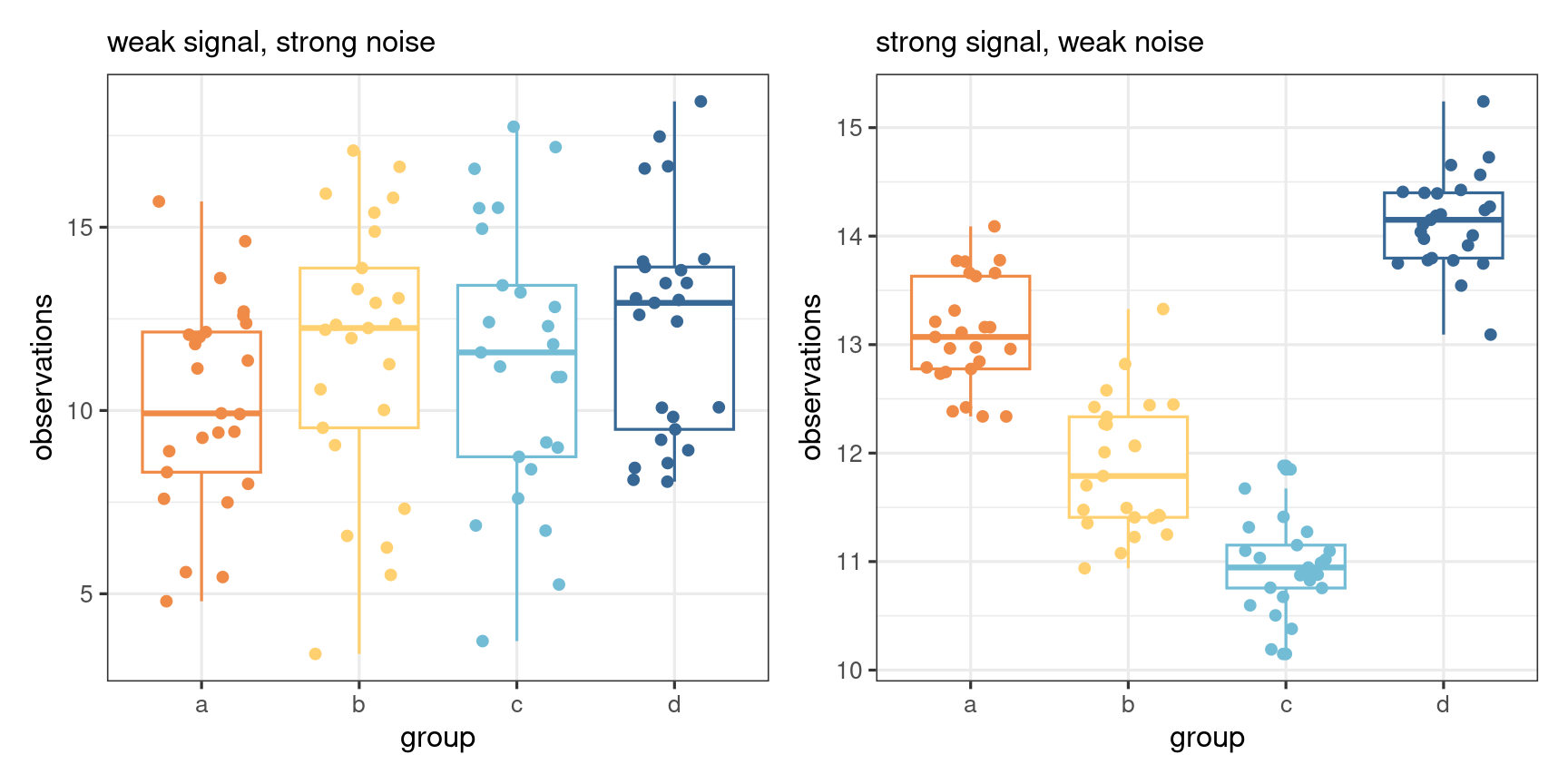
Can you spot the differences?

---

# Information accumulates

<div class="figure" style="text-align: center">
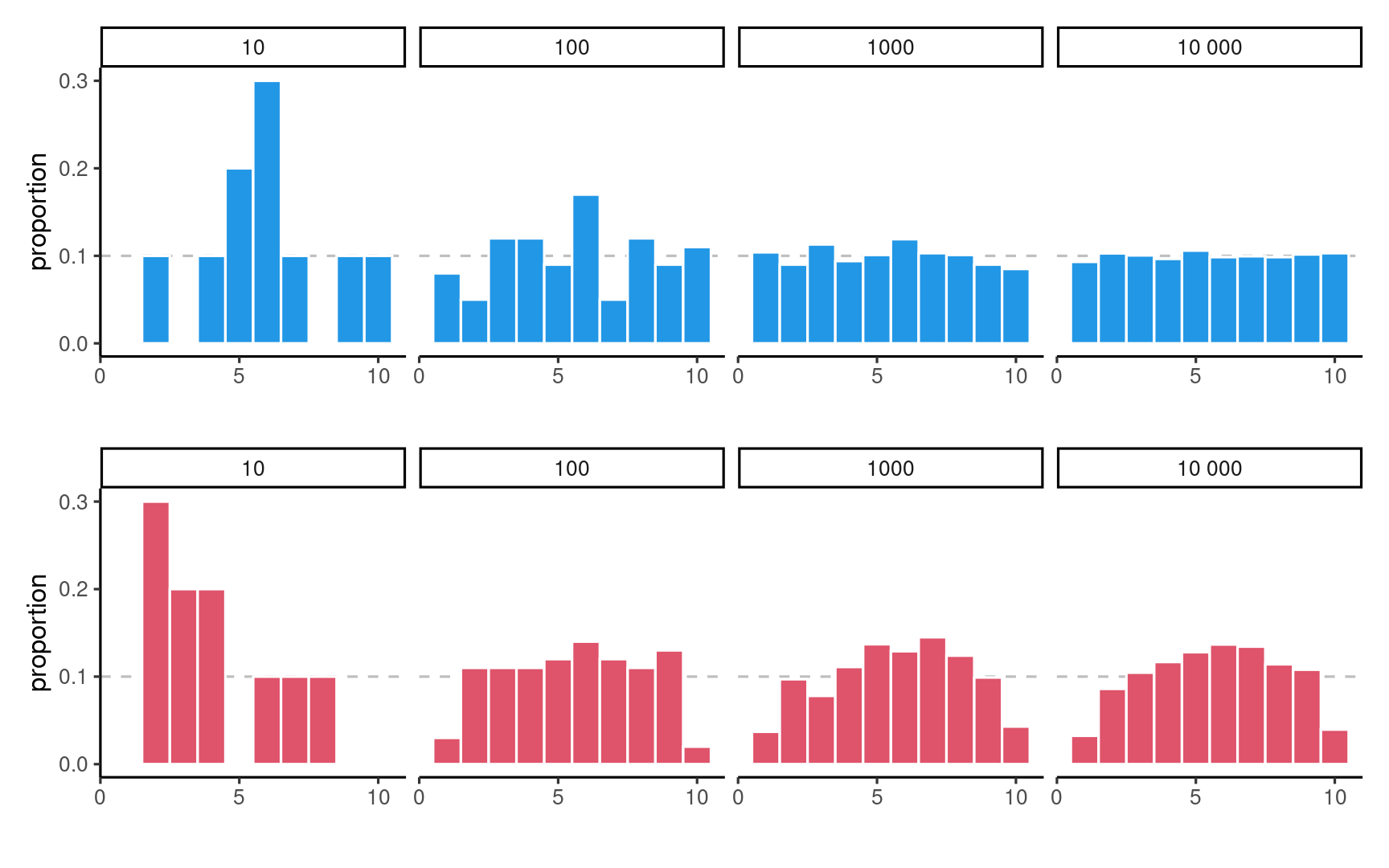
<img src="02-slides_files/figure-html/uniformsamp2-1.png" alt="Histograms of data from uniform (top) and non-uniform (bottom)
distributions with increasing sample sizes." width="576" />
<p class="caption">Histograms of data from uniform (top) and non-uniform (bottom)
distributions with increasing sample sizes.</p>
</div>

---

layout: false
name: hypothesis-tests
class: center middle section-title section-title-4 animated fadeIn

# Hypothesis tests

---

---

# The general recipe of hypothesis testing

.medium[
1. Define variables
2. Write down hypotheses (null/alternative)
3. Choose and compute a test statistic
4. Compare the value to the null distribution (benchmark)
5. Compute the _p_-value
6. Conclude (reject/fail to reject)
7. Report findings

]

---
# Hypothesis tests versus trials

]

- Binary decision: guilty/not guilty
- Summarize evidences (proof)
- Assess evidence in light of **presumption of innocence**
- Verdict: either guilty or not guilty
- Potential for judicial mistakes

]

---

# How to assess evidence?

.box-inv-4.medium.sp-after[statistic = numerical summary of the data.]

.box-inv-4.medium.sp-after[requires benchmark / standardization]

.box-4.sp-after-half[typically a unitless quantity]

.box-4.sp-after-half[need measure of uncertainty of statistic]
---

# General construction principles

.box-inv-4.medium[Wald statistic]

`\begin{align*}
W = \frac{\text{estimated qty} - \text{postulated qty}}{\text{std. error (estimated qty)}}
\end{align*}`

.box-inv-4.sp-after-half[standard error = measure of variability (same units as obs.)]

.box-inv-4.sp-after-half[resulting ratio is unitless!]

???

The standard error is typically function of the sample size and the standard deviation `$\sigma$` of the observations.

---

# Impact of encouragement on teaching

From Davison (2008), Example 9.2

> In an investigation on the teaching of arithmetic, 45 pupils were divided at random into five groups of nine. Groups A and B were taught in separate classes by the usual method. Groups C, D, and E were taught together for a number of days. On each day C were praised publicly for their work, D were publicly reproved and E were ignored. At the end of the period all pupils took a standard test.

---

# Basic manipulations in **R**: load data

``` r
data(arithmetic, package = "hecedsm")
# categorical variable = factor

# Look up data
str(arithmetic)
```

```
## 'data.frame':	45 obs. of  2 variables:
##  $ group: Factor w/ 5 levels "control 1","control 2",..: 1 1 1 1 1 1 1 1 1 2 ...
##  $ score: num  17 14 24 20 24 23 16 15 24 21 ...
```

---

# Basic manipulations in **R**:  summary statistics

``` r
# compute summary statistics
summary_stat <-
  arithmetic |> 
  group_by(group) |>
  summarize(mean = mean(score),
            sd = sd(score))
knitr::kable(summary_stat, 
             digits = 2)
```
]
.pull-right[

|group     |  mean|   sd|
|:---------|-----:|----:|
|control 1 | 19.67| 4.21|
|control 2 | 18.33| 3.57|
|praise    | 27.44| 2.46|
|reprove   | 23.44| 3.09|
|ignore    | 16.11| 3.62|
]

---

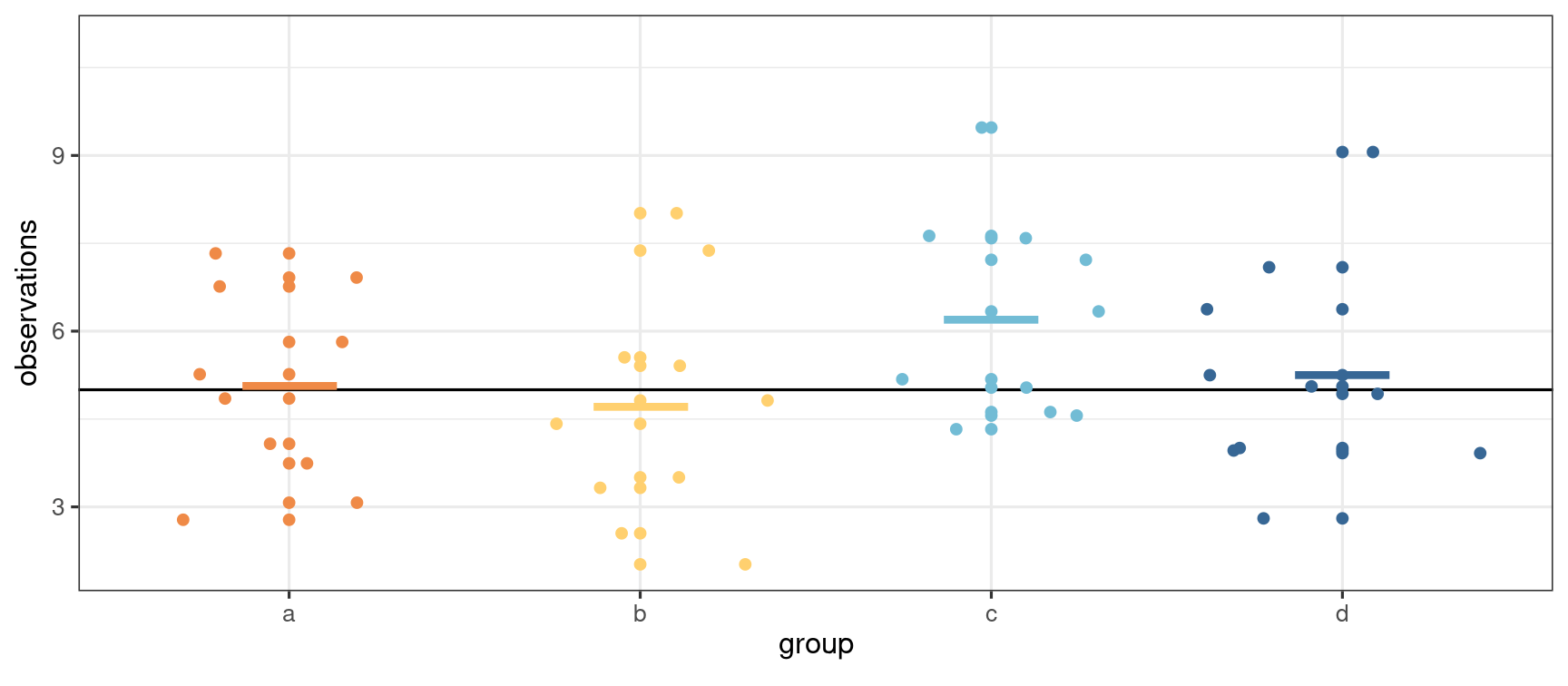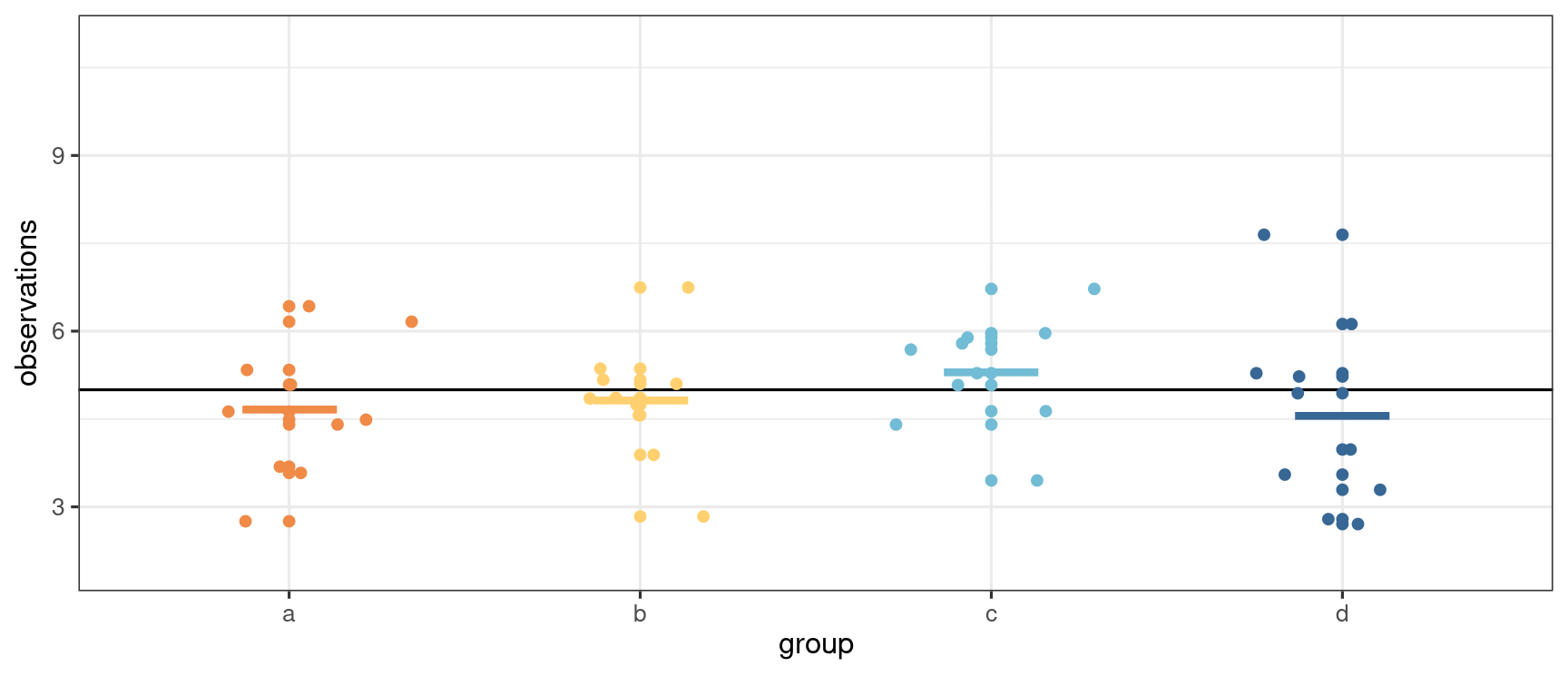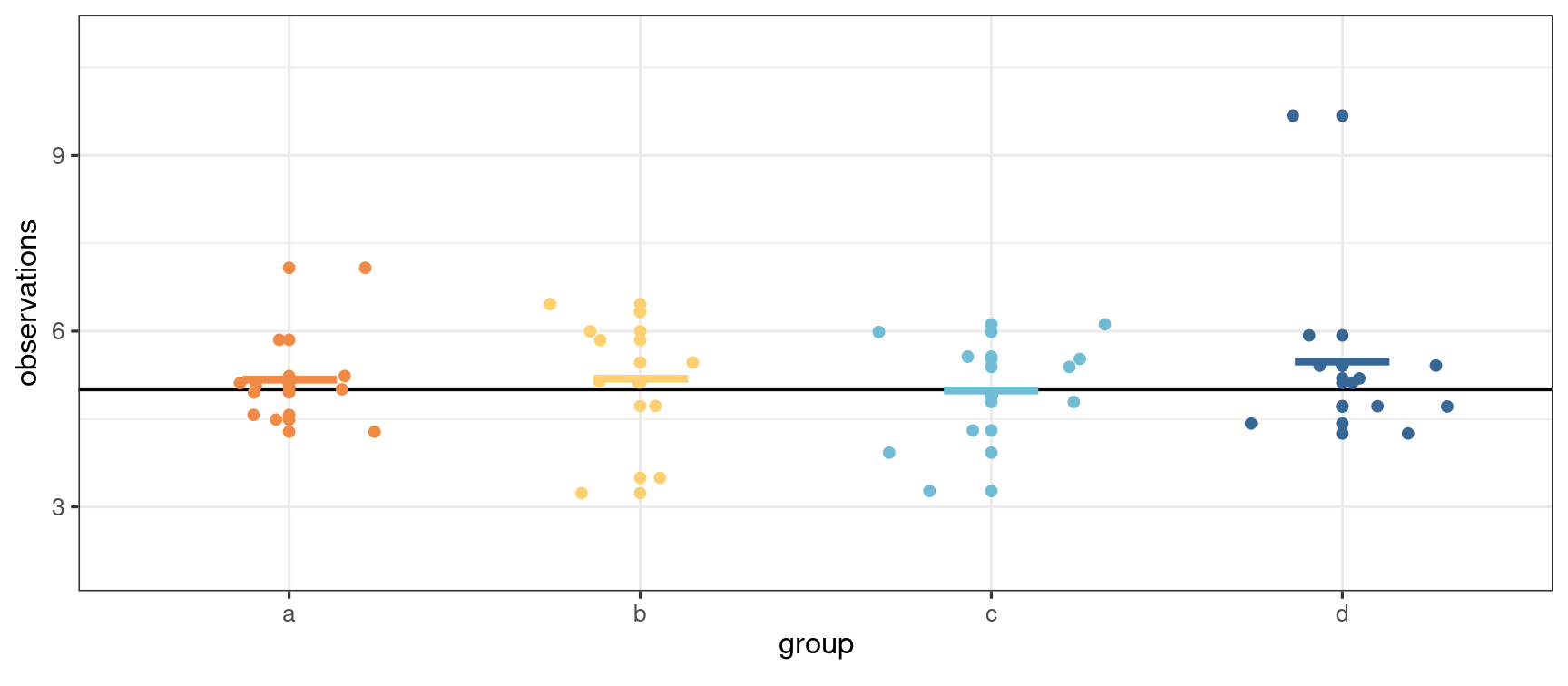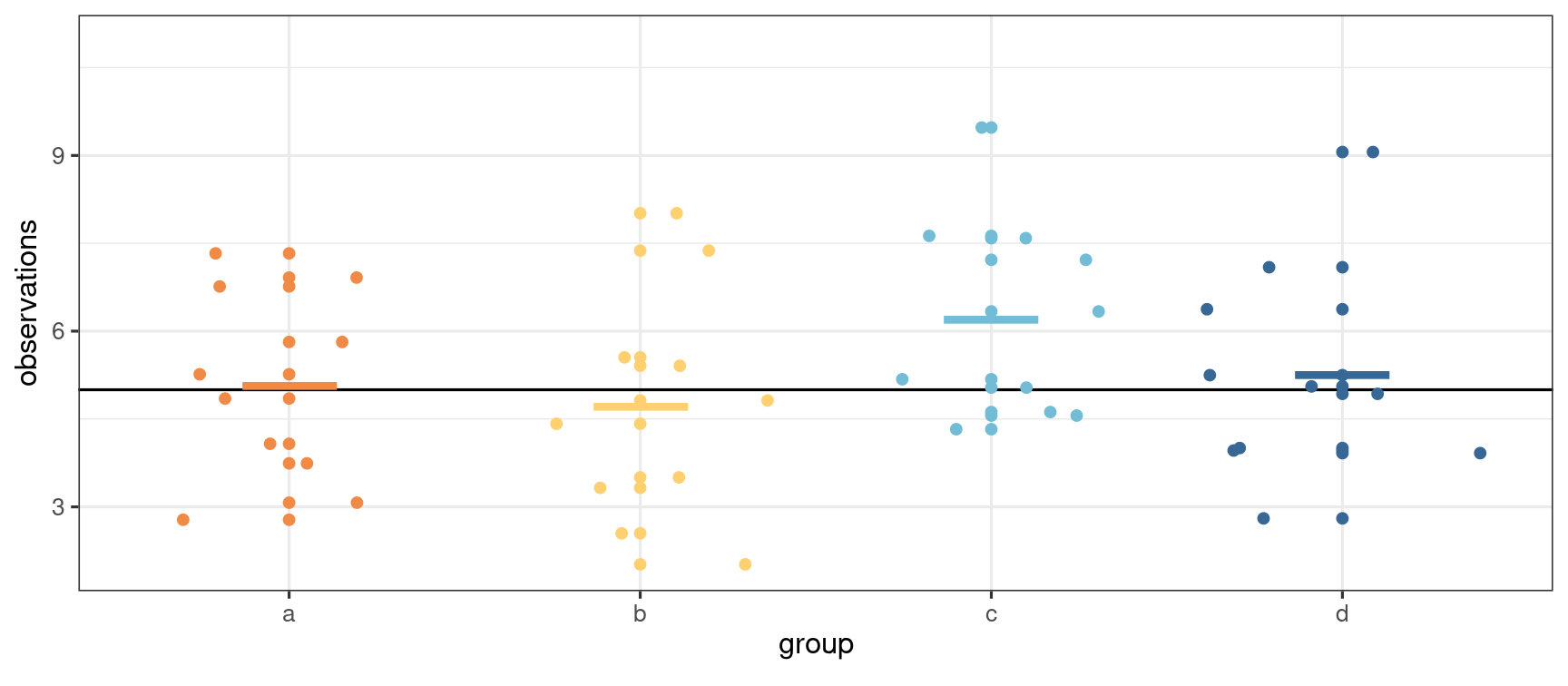
# Basic manipulations in **R**: plot

``` r
# Boxplot with jittered data
ggplot(data = arithmetic,
       aes(x = group,
           y = score)) +
  geom_boxplot() +
  geom_jitter(width = 0.3, 
              height = 0) +
  theme_bw()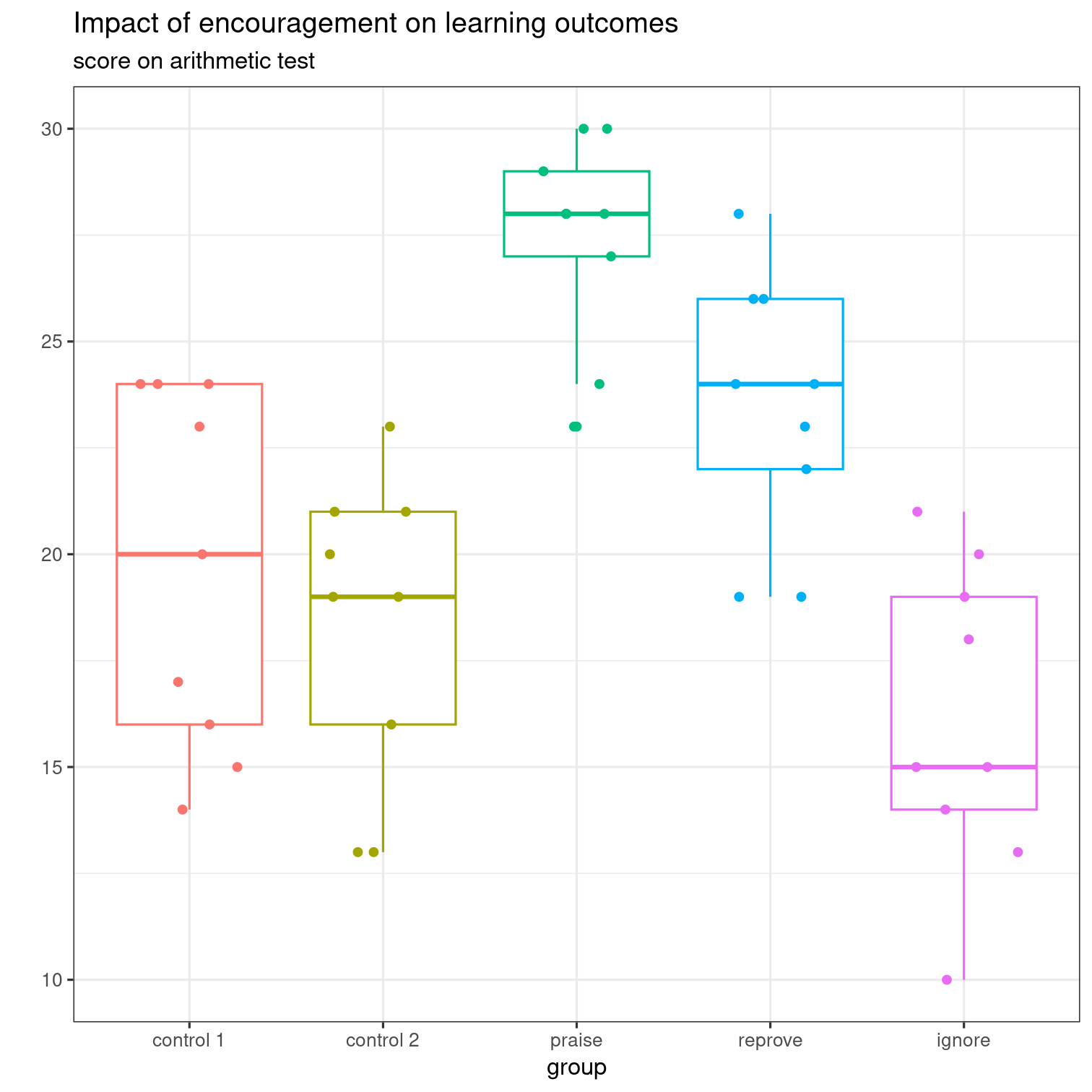
```
]
.pull-right[

]

---

# Formulating an hypothesis

Let `$\mu_{C}$` and `$\mu_{D}$` denote the population average (expectation) score for praise and reprove, respectively.

Our null hypothesis is 
`$$\mathscr{H}_0: \mu_{C} = \mu_{D}$$`
against the alternative `$\mathscr{H}_a$` that they are different (two-sided test).

Equivalent to `$\delta_{CD} = \mu_C - \mu_D = 0$`.

---

# Test statistic

The value of the Wald statistic is 
`$$t=\frac{\widehat{\delta}_{CD} - 0}{\mathsf{se}(\widehat{\delta}_{CD})} = \frac{4}{1.6216}=2.467$$`

???

Could it have happened by chance if there was no difference between groups?

---

# Assessing evidence

--
 
.pull-right[
.box-inv-4.large[Benchmarking]

.medium[
- The same number can have different meanings
    - units matter!
- Meaningful comparisons require some reference.
]
]

---

The null distribution tells us what are the *plausible* values for the statistic and their relative frequency if the null hypothesis holds.

]
.pull-left[

What can we expect to see **by chance** if there is **no difference** between groups?
]

]

???

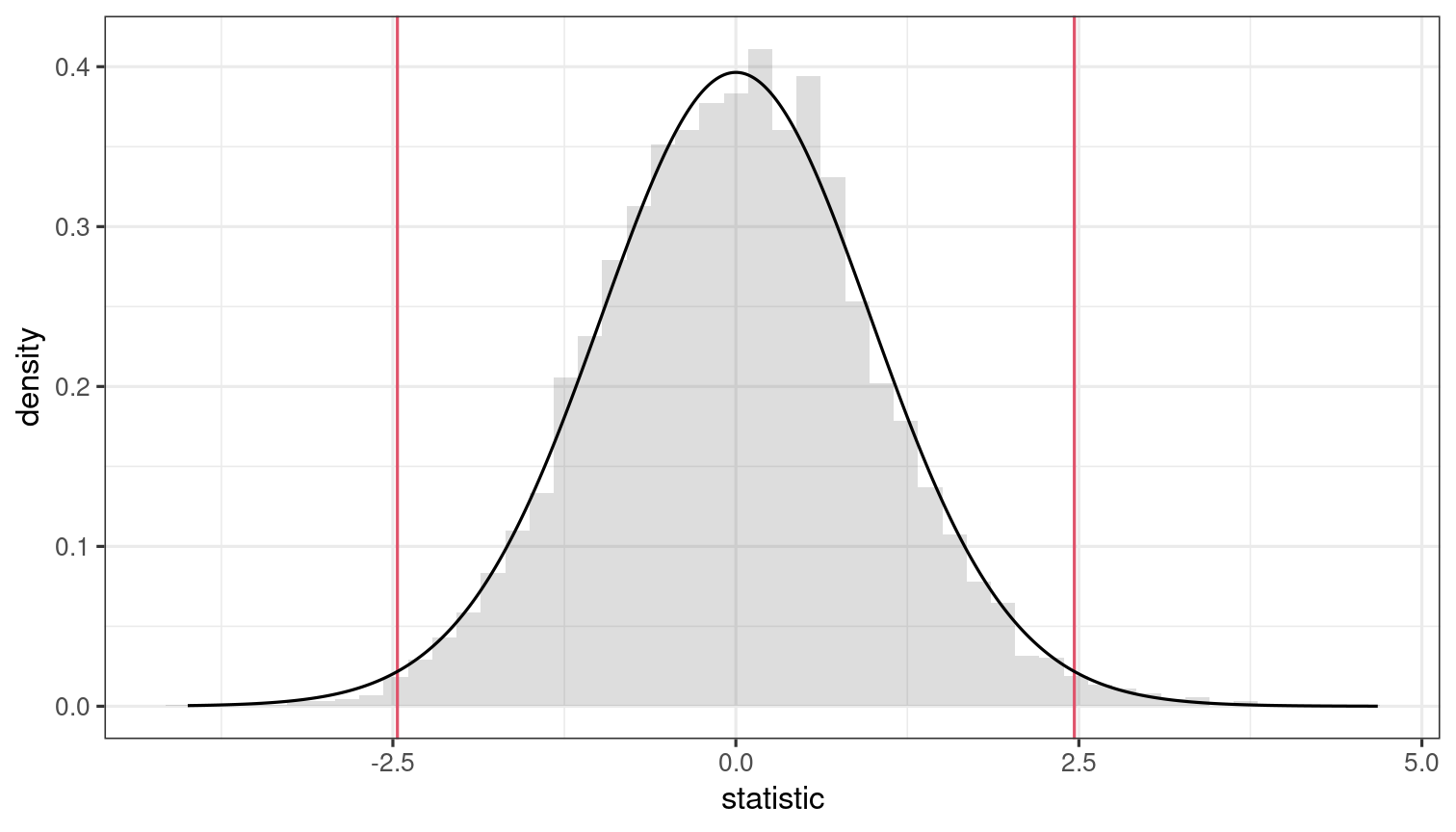
Oftentimes, the null distribution comes with the test statistic

Alternatives include

- Large sample behaviour (asymptotic distribution)
- Resampling/bootstrap/permutation.

---

# _P_-value

- The _p_-value gives the probability of observing an outcome as extreme **if the null hypothesis was true**.

]
.pull-right[
<img src="02-slides_files/figure-html/nulltopval-1.png" width="432" style="display: block; margin: auto;" />
]

???

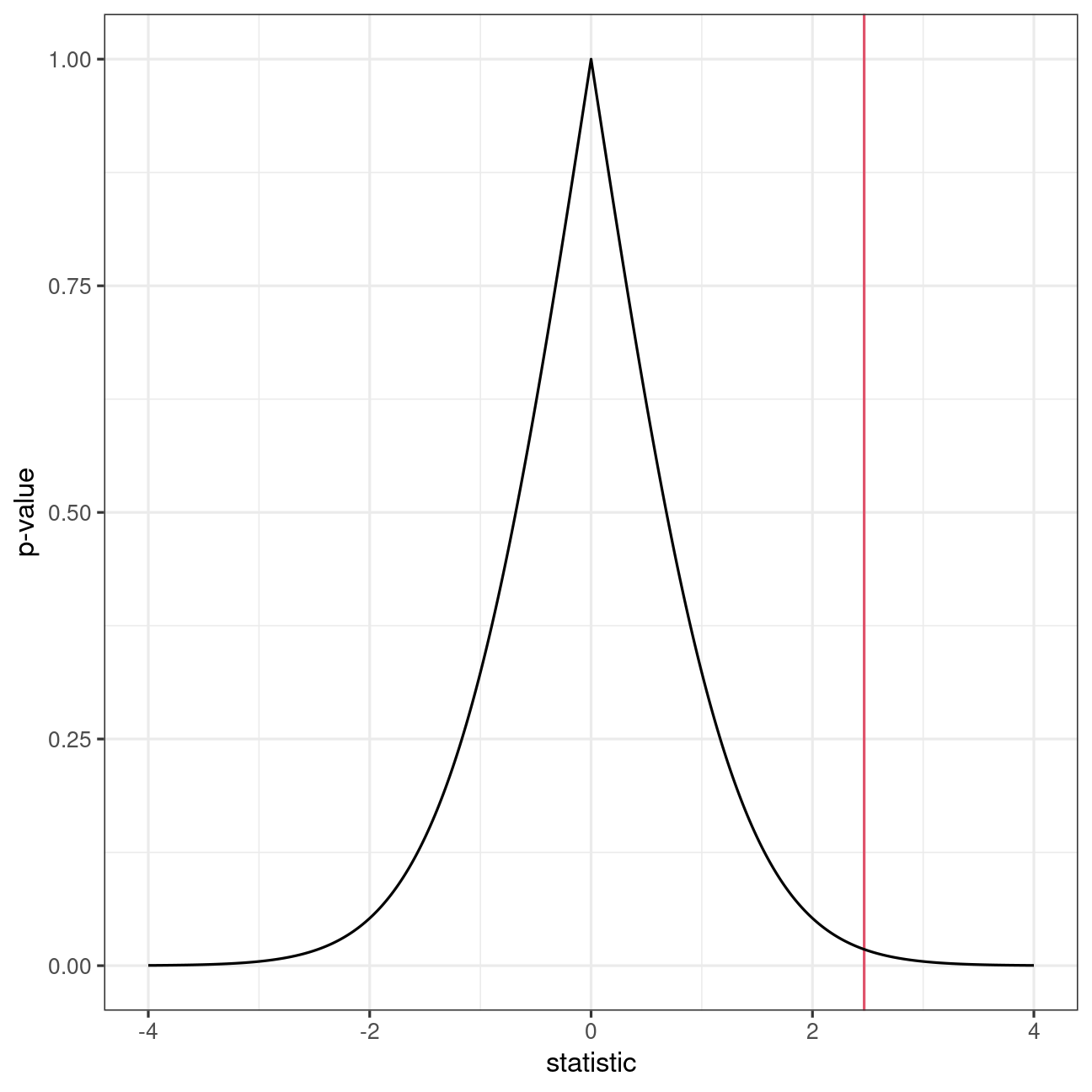
Uniform distribution under H0

---

# Level = probability of condemning an innocent

.box-4.sp-after-half.medium[
Fix **level** `$\alpha$`
**before** the experiment.
]

.box-inv-4.sp-after-half.medium[

Choose small `$\alpha$` (typical value is 5%)
]

.box-4.sp-after-half.medium[
Reject `$\mathscr{H}_0$` if p-value less than `$\alpha$`
]

???

Question: why can't we fix `$\alpha=0$`?

---

# What is really a _p_-value?

The [American Statistical Association (ASA)](https://doi.org/10.1080/00031305.2016.1154108) published a statement on
(mis)interpretation of p-values.

> (2) P-values do not measure the probability that the studied hypothesis is true

> (3) Scientific conclusions and business or policy decisions should not be based only on whether a p-value passes a specific threshold.

>(4) P-values and related analyses should not be reported selectively

> (5) P-value, or statistical significance, does not measure the size of an effect or the importance of a result
---

# Reporting results of a statistical procedure

Nature's checklist

---

layout: false
name: hypothesis-tests
class: center middle section-title section-title-5 animated fadeIn

# Pairwise comparisons

---

---

# Pairwise differences and _t_-tests

The _p_-values and confidence intervals for pairwise differences between groups `$j$` and `$k$` are based on the _t_-statistic:

`\begin{align*}
t = \frac{\text{estimated} - \text{postulated difference}}{\text{uncertainty}}= \frac{(\widehat{\mu}_j - \widehat{\mu}_k) - (\mu_j - \mu_k)}{\mathsf{se}(\widehat{\mu}_j - \widehat{\mu}_k)}.
\end{align*}`

In large sample, this statistic behaves like a Student-_t_ variable with `$n-K$` degrees of freedom, denoted `$\mathsf{St}(n-K)$` hereafter.

Note: in an analysis of variance model, the standard error `$\mathsf{se}(\widehat{\mu}_j - \widehat{\mu}_k)$` is based the pooled variance estimate (estimated using all observations).

]
---

# Pairwise differences

Consider the pairwise average difference in scores between the praise (group C) and the reprove (group D) of the `arithmetic` data.

- Group sample averages are `$\widehat{\mu}_C = 27.4$` and `$\widehat{\mu}_D = 23.4$`
- The estimated average difference between groups `$C$` and `$D$` is `$\widehat{\delta}_{CD} = 4$`
- The estimated pooled *standard deviation* for the five groups is `$1.15\vphantom{\widehat{\delta}_{CD}}$`
- The *standard error* for the pairwise difference is `$\mathsf{se}(\widehat{\delta}_{CD}) = 1.6216$`
- There are `$n=45$` observations and `$K=5$` groups

---

# _t_-tests: null distribution is Student-_t_

If we postulate `$\delta_{jk} = \mu_j - \mu_k = 0$`, the test statistic becomes

`\begin{align*}
t = \frac{\widehat{\delta}_{jk} - 0}{\mathsf{se}(\widehat{\delta}_{jk})}
\end{align*}`

The `$p$`-value is `$p = 1- \Pr(-|t| \leq T \leq |t|)$` for `$T \sim \mathsf{St}_{n-K}$`.
   - probability of statistic being more extreme than `$t$`

Recall: the larger the values of the statistic `$t$` (either positive or negative), the more evidence against the null hypothesis.

---

# Critical values

For a test at level `$\alpha$` (two-sided), we fail to reject null hypothesis for all values of the test statistic `$t$` that are in the interval

`$$\mathfrak{t}_{n-K}(\alpha/2) \leq t \leq \mathfrak{t}_{n-K}(1-\alpha/2)$$`

Because of the symmetry around zero, `$\mathfrak{t}_{n-K}(1-\alpha/2) = -\mathfrak{t}_{n-K}(\alpha/2)$`.

- We call `$\mathfrak{t}_{n-K}(1-\alpha/2)$` a **critical value**. 
- in **R**, the quantiles of the Student _t_ distribution are obtained from `qt(1-alpha/2, df = n - K)` where `n` is the number of observations and `K` the number of groups.

---

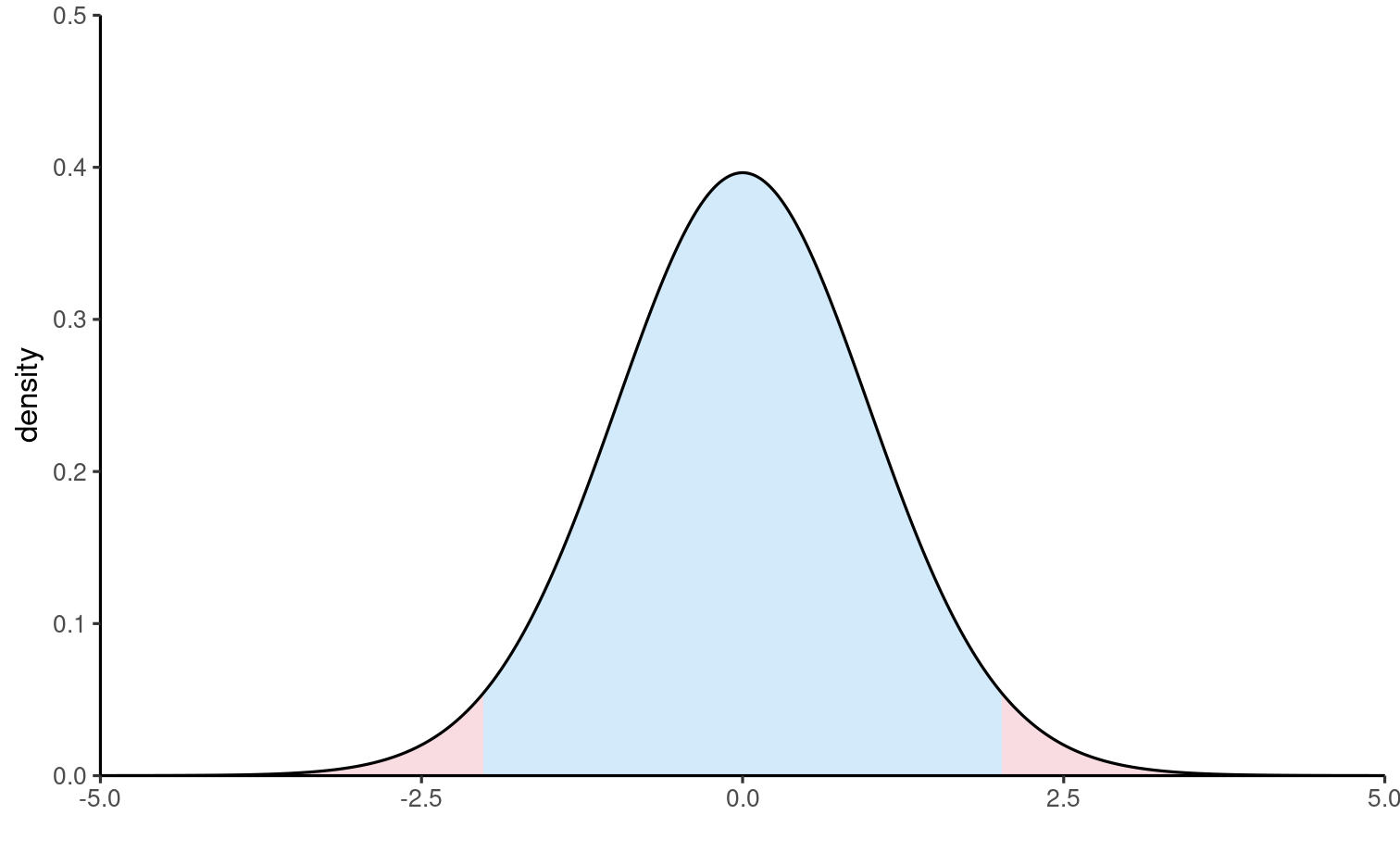
# Null distribution

The blue area defines the set of values for which we fail to reject null `$\mathscr{H}_0$`.

All values of `$t$` falling in the red area lead to rejection at level `$5$`%.

---

# Example

- If `$\mathscr{H}_0: \delta_{CD}=0$`, the `$t$` statistic is 
`$$t=\frac{\widehat{\delta}_{CD} - 0}{\mathsf{se}(\widehat{\delta}_{CD})} = \frac{4}{1.6216}=2.467$$`
- The `$p$`-value is `$p=0.018$`. 
- We reject the null at level `$\alpha=5$`% since `$0.018 < 0.05$`.
- Conclude that there is a significant difference at level `$\alpha=0.05$` between the average scores of subpopulations `$C$` and `$D$`.

---

# Confidence interval

Let `$\delta_{jk}=\mu_j - \mu_k$` denote the population difference, `$\widehat{\delta}_{jk}$` the estimated difference (difference in sample averages) and `$\mathsf{se}(\widehat{\delta}_{jk})$` the estimated standard error.

The region for which we fail to reject the null is 
`\begin{align*}
-\mathfrak{t}_{n-K}(1-\alpha/2) \leq  \frac{\widehat{\delta}_{jk} - \delta_{jk}}{\mathsf{se}(\widehat{\delta}_{jk})} \leq \mathfrak{t}_{n-K}(1-\alpha/2)
\end{align*}`
which rearranged gives the `$(1-\alpha)$` confidence interval for the (unknown) difference `$\delta_{jk}$`.

`\begin{align*}
\widehat{\delta}_{jk} - \mathsf{se}(\widehat{\delta}_{jk})\mathfrak{t}_{n-K}(1-\alpha/2) \leq \delta_{jk} \leq \widehat{\delta}_{jk} + \mathsf{se}(\widehat{\delta}_{jk})\mathfrak{t}_{n-K}(1-\alpha/2)
\end{align*}`

]

---
class: title title-2

# Interpretation of confidence intervals

The reported confidence interval is of the form

$$ \text{estimate} \pm \text{critical value} \times \text{standard error}$$

.box-5.sp-after-half[ confidence interval = [lower, upper] units]

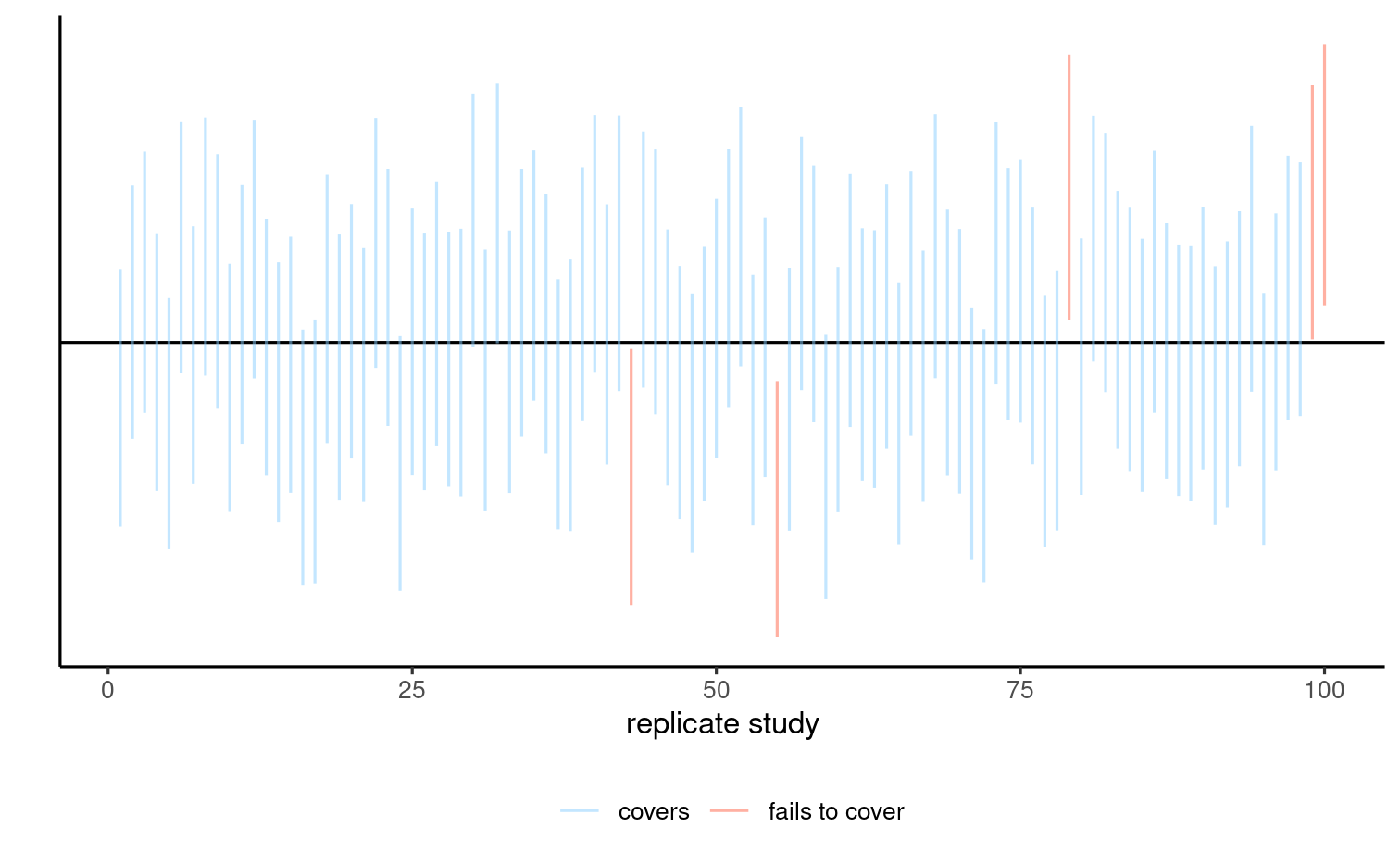
If we replicate the experiment and compute confidence intervals each time
- on average, 95% of those intervals will contain the true value if the assumptions underlying the model are met.

---
class: title title-2

# Interpretation in a picture: coin toss analogy
.small[
Each interval either contains the true value (black horizontal line) or doesn't.
]
<img src="02-slides_files/figure-html/unnamed-chunk-6-1.png" alt="100 confidence intervals" width="70%" style="display: block; margin: auto;" />
---

# Why confidence intervals?

Test statistics are standardized, 
- Good for comparisons with benchmark
- typically meaningless (standardized = unitless quantities)

Two options for reporting:

- `$p$`-value: probability of more extreme outcome if no mean difference
- confidence intervals: set of all values for which we fail to reject the null hypothesis at level `$\alpha$` for the given sample

---

# Example

- Mean difference of `$\widehat{\delta}_{CD}=4$`,  with `$\mathsf{se}(\widehat{\delta}_{CD})=1.6216$`.
- The critical values for a test at level `$\alpha = 5$`% are `$-2.021$` and `$2.021$` 
   - `qt(0.975, df = 45 - 5)`
- Since `$|t| > 2.021$`, reject `$\mathscr{H}_0$`: the two population are statistically significant at level `$\alpha=5$`%.
- The confidence interval is `$$[4-1.6216\times 2.021, 4+1.6216\times 2.021] = [0.723, 7.277]$$`

The postulated value `$\delta_{CD}=0$` is not in the interval: reject `$\mathscr{H}_0$`.

---

# Pairwise differences in **R**

``` r
library(emmeans) # marginal means and contrasts
model <- aov(score ~ group, data = arithmetic)
margmeans <- emmeans(model, specs = "group")
contrast(margmeans, 
         method = "pairwise",
         adjust = 'none', 
         infer = TRUE) |>
  as_tibble() |>
  filter(contrast == "praise - reprove") |>
  knitr::kable(digits = 3)
```

|contrast         | estimate|    SE| df| lower.CL| upper.CL| t.ratio| p.value|
|:----------------|--------:|-----:|--:|--------:|--------:|-------:|-------:|
|praise - reprove |        4| 1.622| 40|    0.723|    7.277|   2.467|   0.018|

---

---

# Recap 1
.medium[

- Testing procedures factor in the uncertainty inherent to sampling.
- Adopt particular viewpoint: null hypothesis (simpler model, e.g., no difference between group) is true. We consider the evidence under that optic.

]

---

# Recap 2

- _p_-values  measures compatibility with the null model (relative to an alternative)
- Tests are standardized values,

The output is either a _p_-value or a confidence interval
   - confidence interval: on scale of data (meaningful interpretation)
   - _p_-values: uniform on [0,1] if the null hypothesis is true
   
]
---

# Recap 3

- All hypothesis tests share common ingredients
- Many ways, models and test can lead to the same conclusion.
- Transparent reporting is important!

]