Contrasts and multiple testing

# Contrasts and multiple testing

**Session 4**

]

---

# Outline
--

.box-3.medium.sp-after-half[Contrasts]

.box-6.medium.sp-after-half[Multiple testing]

---

---

# Planned comparisons

- Oftentimes, we are not interested in the global null hypothesis.
- Rather, we formulate planned comparisons *at registration time* for effects of interest

.box-inv-3.large[What is the scientific question of interest?]

---
# Global null vs contrasts

<img src="img/04/Dim_lighting.png" width="75%" style="display: block; margin: auto;" />
.box-3.sp-after-half[Global test]
]

.box-3.box-3.sp-after-half[Contrasts]

]

???

Analogy here is that the global test is a dim light: it shows there are differences, but does not tell us where. Contrasts are more specific.
---
# Linear contrasts

With `$K$` groups, null hypothesis of the form

`$$\mathscr{H}_0: \underset{\text{weighted sum of subpopulation means}}{C = c_1 \mu_1 + \cdots + c_K\mu_K} =a$$`
--

.box-3.medium.sp-after[
Linear combination of weighted group averages
]
---

# Examples of linear contrasts

.box-inv-3.sp-after-half[
Global mean larger than `$a$`?

]

`$$\mathscr{H}_0: \frac{n_1}{n} \mu_1 + \cdots + \frac{n_K}{n} \mu_K  \leq a$$`

.box-inv-3.sp-after-half[
Pairwise comparison
]

`$$\mathscr{H}_0: \mu_i = \mu_j, \quad i \neq j$$`

---

# Characterization of linear contrasts

- Weights `$c_1, \ldots, c_K$` are specified by the **user**.
- Mean response in each experimental group is estimated as sample average of observations in that group, `$\widehat{\mu}_1, \ldots, \widehat{\mu}_K$`.
- Assuming equal variance, the contrast statistic behaves in large samples like a Student-_t_ distribution with `$n-K$` degrees of freedom.

---
# Sum-to-zero constraint

.medium.center[

If `$c_1 + \cdots+c_K = 0$`, the contrast encodes

rather than information about the overall mean.
]

---

# Arithmetic example

.box-3.medium[Setup]

.pull-left-3[
.box-inv-3[
group 1 
]
.center[
(control)
]
]
.pull-middle-3[
.box-inv-3.sp-after-half[
group 2 
]
.center[
(control)
]
]

.box-3.medium[Hypotheses of interest]

- `$\mathscr{H}_{01}: \mu_{\text{praise}} = \mu_{\text{reproved}}$` (attention)
- `$\mathscr{H}_{02}: \frac{1}{2}(\mu_{\text{control}_1}+\mu_{\text{control}_2}) = \mu_{\text{praised}}$` (encouragement)

???

This is post-hoc, but supposed we had particular interest in the following hypothesis (for illustration purposes)

---

# Contrasts

With placeholders for each group, write
`$\mathscr{H}_{01}: \mu_{\text{praised}} = \mu_{\text{reproved}}$` as 
.small.center[

`$0\cdot \mu_{\text{control}_1}$` + `$0\cdot \mu_{\text{control}_2}$` + `$1 \cdot \mu_{\text{praised}}$` - `$1\cdot \mu_{\text{reproved}}$` + `$0 \cdot \mu_{\text{ignored}}$`

]

The sum of the coefficient vector, `$\boldsymbol{c} = (0, 0, 1, -1, 0)$`, is zero.

Similarly, for `$\mathscr{H}_{02}: \frac{1}{2}(\mu_{\text{control}_1}+\mu_{\text{control}_2}) = \mu_{\text{praise}}$`

`$$\frac{1}{2} \cdot \mu_{\text{control}_1} + \frac{1}{2}\cdot \mu_{\text{control}_2} - 1 \cdot \mu_{\text{praised}} + 0\cdot \mu_{\text{reproved}} + 0 \cdot \mu_{\text{ignored}}$$`

The contrast vector is `$\boldsymbol{c}=\left(\frac{1}{2}, \frac{1}{2}, -1, 0, 0\right)$`; entries again sum to zero.

Equivalent formulation is obtained by picking `$\boldsymbol{c} = (1,1,-2,0,0)$`

---
# Contrasts in **R** with `emmeans`

```r
library(emmeans)
linmod <- lm(score ~ group, data = arithmetic)
linmod_emm <- emmeans(linmod, specs = 'group')
contrast_specif <- list(
 controlvspraised = c(0.5, 0.5, -1, 0, 0),
 praisedvsreproved = c(0, 0, 1, -1, 0)
)
contrasts_res <- 
 contrast(object = linmod_emm, 
 method = contrast_specif)
# Obtain confidence intervals instead of p-values
confint(contrasts_res)
```
---
# Output

|contrast | null.value| estimate| std.error| df| statistic|p.value |
|:------------------|----------:|--------:|---------:|--:|---------:|:-------|
|control vs praised | 0| -8.44| 1.40| 40| -6.01|<1e-04 |
|praised vs reprove | 0| 4.00| 1.62| 40| 2.47|0.018 |

|contrast           |  lower| upper|
|:------------------|------:|-----:|
|control vs praised | -11.28| -5.61|
|praised vs reprove |   0.72|  7.28|

---
# One-sided tests

Suppose we postulate that the contrast statistic is **bigger** than some value `$a$`.

- The alternative is `$\mathscr{H}_a: C>a$` (what we are trying to prove)!
- The null hypothesis is therefore `$\mathscr{H}_0: C \leq a$` (Devil's advocate)

It suffices  to consider the endpoint `$C = a$` (why?)

- If we reject `$C=a$` in favour of `$C>a$`, all other values of the null hypothesis are even less compatible with the data.

---
# Comparing rejection regions

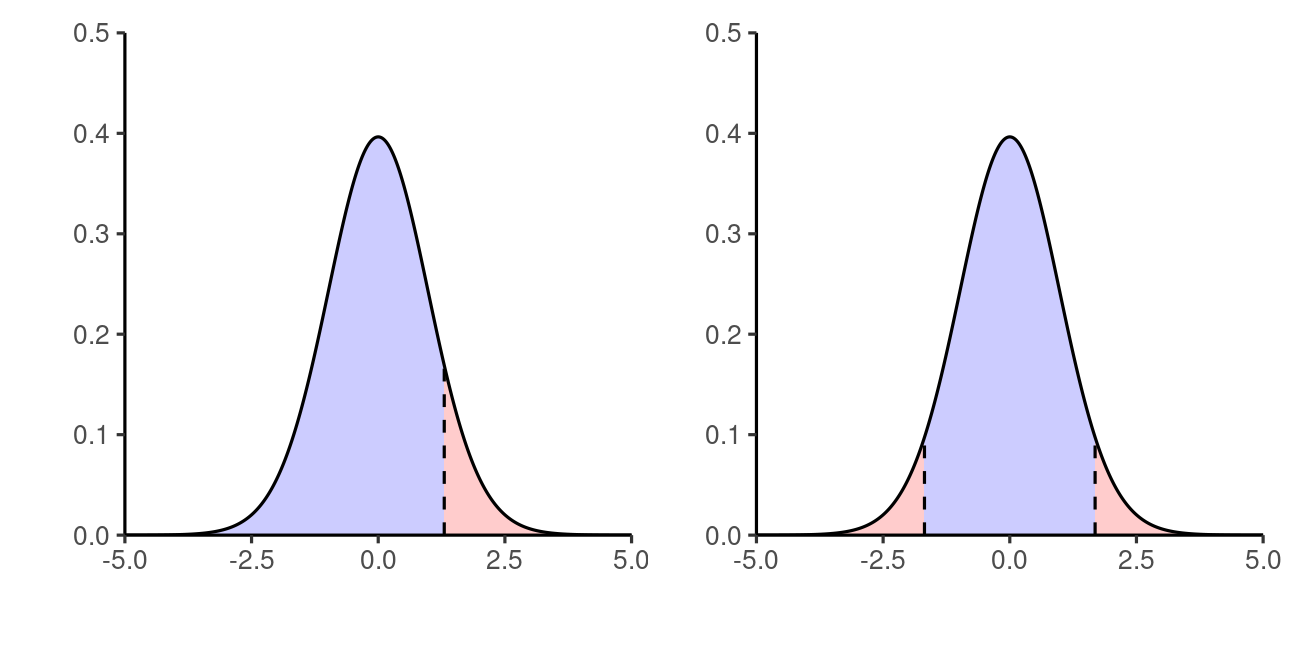
Rejection regions for a one-sided test (left) and a two-sided test (right).

---

# When to use one-sided tests?

In principle, one-sided tests are more powerful (larger rejection region on one sided).

- However, important to **pre-register** hypothesis
   - can't look at the data before formulating the hypothesis (as always)!
- More logical for follow-up studies and replications.

If you postulate `$\mathscr{H}_a: C>a$` and the data show the opposite with `$\widehat{C} \leq a$`, then the `$p$`-value for the one-sided test is 1!

---

layout: false
name: multiple-testing
class: center middle section-title section-title-6 animated fadeIn

# Multiple testing

---

---
# *Post-hoc* tests

Suppose you decide to look at all pairwise differences

.box-inv-6.medium[
Comparing all pairwise differences: `$m=\binom{K}{2}$` tests
]

- `$m=3$` tests if `$K=3$` groups,
- `$m=10$` tests if `$K=5$` groups,
- `$m=45$` tests if `$K=10$` groups...

???

The recommendation for ANOVA is to limit the number of tests to the number of subgroups

---

# There is a catch...

Read the small prints:

.center.medium[
If you do a **single** hypothesis test and
 your testing procedure is well calibrated
 (*meaning the model assumptions are met*), 
 there is a probability `$\alpha$`
 of making a type I error
 if the null hypothesis is true.
]

---

# How many tests?

Dr. Yoav Benjamini looked at the number of tests performed in the Psychology replication project

.small[
[Open Science Collaboration. (2015). Estimating the reproducibility of psychological science. Science, 349(6251), aac4716.](https://doi.org/10.1126/science.aac4716)
]

The number of tests performed ranged from 4 to 700, with an average of 72.

Most studies did not account for selection.

???

Yoav B. reported that 11/100 engaged with selection, but only cursorily

---

# Scientifist, investigate!

- Consider the Cartoon *Significant* by Randall Munroe (https://xkcd.com/882/)

.center.small[
![](img/04/xkcd_882_4.png)

]
.small[
It highlights two problems: lack of accounting for multiple testing and selective reporting.
]

???

Bring students to realize the multiple testing problem: quiz them on potential consequences

Gone fishing

- Having found no difference between group, you decide to stratify with another categorical variable and perform the comparisons for each level (subgroup analysis)
 
The more tests you perform, the larger the type I error.

---

# Probability of type I error

If we do `$m$` **independent** comparisons, each
one at the level `$\alpha$`, the probability of making at least one type I error, say `$\alpha^{\star}$`, is

$$
\alpha^{\star} = 
1 – \text{probability of making no type I error} = 1- (1-\alpha)^m.
$$

With `$\alpha = 0.05$`
- `$m=4$` tests, `$\alpha^{\star} \approx 0.185$`.
- `$m=72$` tests, `$\alpha^{\star} \approx 0.975$`.

]
???

The first equality holds under the assumption observations (and thus tests) are independent, the second follows from Boole's inequality and does not require independence.

It is an upper bound on the probability of making no type I error

---

# Statistical significance at the 5% level

Why `$\alpha=5$`%? Essentially **arbitrary**...

> If one in twenty does not seem high enough odds, we may, if we prefer it, draw the line at one in fifty or one in a hundred. Personally, the writer prefers to set a low standard of significance at the 5 per cent point, and ignore entirely all results which fails to reach this level.

.small[
Fisher, R.A. (1926). The arrangement of field experiments. *Journal of the
Ministry of Agriculture of Great Britain*, 33:503-513.
]

---

# Family of hypothesis

Consider `$m$` tests with the corresponding null hypotheses `$\mathscr{H}_{01}, \ldots, \mathscr{H}_{0m}$`.

- The family may depend on the context, but including any hypothesis that is scientifically relevant and could be reported.

.box-inv-6.wide.sp-after-half[
**Should be chosen a priori and pre-registered**
]

**Keep it small**: the number of planned comparisons for a one-way ANOVA should be less than the number of groups `$K$`.

???

Researchers do not all agree with this “liberal” approach (i.e., that don't correct for multiplicity even for pre-planned comparisons) and recommend to always control for the familywise or experimentwise Type I error rate. *dixit F. Bellavance*.
---

# Notation

Define indicators
`$$\begin{align}R_i &= \begin{cases} 1 & \text{if we reject }  \mathscr{H}_{0i} \\
0 & \text{if we fail to reject } \mathscr{H}_{0i}
\end{cases}\\
V_i &=\begin{cases} 1 & \text{type I error for } \mathscr{H}_{0i}\quad  (R_i=1 \text{ and  }\mathscr{H}_{0i} \text{ is true}) \\ 0 & \text{otherwise} 
\end{cases}
\end{align}$$`

with 
- `$R=R_1 + \cdots + R_m$` the total number of rejections ( `$0 \leq R \leq m$` ).
- `$V = V_1 + \cdots + V_m$` the number of null hypothesis rejected by mistake.

---

**Definition**: the familywise error rate is the probability of making at least one type I error per family

`$$\mathsf{FWER} = \Pr(V \geq 1)$$`

If we use a procedure that controls for the family-wise error rate, we talk about .color-6[simultaneous inference] (or simultaneous coverage  for confidence intervals).

---

# Bonferroni's procedure

Consider a family of `$m$` hypothesis tests and perform each test at level `$\alpha/m$`.
- reject `$i$`th null `$\mathscr{H}_{i0}$` if the associated _p_-value `$p_i \leq \alpha/m$`.
- build confidence intervals similarly with `$1-\alpha/m$` quantiles.

If the (raw) `$p$`-values are reported, reject `$\mathscr{H}_{0i}$` if `$m \times p_i \leq \alpha$` (i.e., multiply reported `$p$`-values by `$m$`)

???

Often incorrectly applied to a set of significant contrasts, rather than for preplanned comparisons only

---

# Holm's sequential method

Order the `$p$`-values of the family of `$m$` tests from smallest to largest
`$$p_{(1)} \leq \cdots \leq p_{(m)}$$`

associated to null hypothesis `$\mathscr{H}_{0(1)}, \ldots, \mathscr{H}_{0(m)}$`.

**Idea** use a different level for each test, more stringent for smaller `$p$`-values.

Coupling Holm's method with Bonferroni's procedure: compare `$p_{(1)}$` to `$\alpha_{(1)} = \alpha/m$`, `$p_{(2)}$` to `$\alpha_{(2)}=\alpha/(m-1)$`, etc.

.box-inv-6.sp-after-half[
Holm-Bonferroni procedure is **always** more powerful than Bonferroni
]

---

# Sequential Holm-Bonferroni procedure

.medium[
 
0. order `$p$`-values from smallest to largest.
1. start with the smallest `$p$`-value.
2. check significance one test at a time.
3. stop when the first non-significant `$p$`-value is found or no more test.

]

---

# Conclusion for Holm-Bonferroni

Reject smallest _p_-values until you find one that fails, reject rest

If `$p_{(j)} \geq \alpha_{(j)}$` but `$p_{(i)} < \alpha_{(i)}$` for `$i=1, \ldots, j-1$` (all smaller `$p$`-values)
- reject `$\mathscr{H}_{0(1)}, \ldots, \mathscr{H}_{0(j-1)}$`
- fail to reject `$\mathscr{H}_{0(j)}, \ldots, \mathscr{H}_{0(m)}$`
]
.pull-right[

All _p_-values are lower than their respective cutoff:

If `$p_{(i)} \leq \alpha_{(i)}$` for all test `$i=1, \ldots, m$`
- reject `$\mathscr{H}_{0(1)}, \ldots, \mathscr{H}_{0(m)}$`
]

---
class: title title-6
# Numerical example

Consider `$m=3$` tests with raw `$p$`-values `$0.01$`, `$0.04$`, `$0.02$`.

`$i$` | `$p_{(i)}$` | `$\text{Bonferroni}$` | `$\text{Holm-Bonferroni}$`
--------|--------|---------|---------
1 | `$0.01$` | `$3 \times 0.01 = 0.03$` | `$3 \times 0.01 = 0.03$`
2 | `$0.02$` | `$3 \times 0.02 = 0.06$` | `$2 \times 0.02 = 0.04$`
3 | `$0.04$` | `$3 \times 0.04 = 0.12$` | `$1 \times 0.04 = 0.04$`

Reminder of Holm–Bonferroni:  multiply by `$(m-i+1)$` the `$i$`th smallest `$p$`-value `$p_{(i)}$`, compare the product to `$\alpha$`.

]

---

# Why choose Bonferroni's procedure?

- `$m$` must be prespecified
- simple and generally applicable (any design)
- but dominated by sequential procedures (Holm-Bonferroni uniformly more powerful)
- low power when the number of test `$m$` is large
- also controls for the expected number of false positive, `$\mathsf{E}(V)$`, a more stringent criterion called **per-family error rate** (PFER)

.small[
**Careful**: adjust for the real number of comparisons made (often reporter just correct only the 'significant tests', which is wrong).
]

???

# Controlling the average number of errors

The FWER does not make a distinction between one or multiple type I errors.

We can also look at a more stringent criterion

.box-inv-6.sp-after-half[**per-family error rate** (PFER)]
.box-inv-6[i.e., the expected number of false positive]

Since 
`$$\mathsf{FWER} = \Pr(V \geq 1) \leq \mathsf{E}(V) = \mathsf{PFER}$$`

.small[any procedure that controls the per-family error rate also controls the familywise error rate.]
Bonferroni controls both per-family error rate and family-wise error rate.
---

# Confidence intervals for linear contrasts

Given a linear contrast of the form `$$C=c_1\mu_1 + \cdots + c_K\mu_K$$` with `$c_1 + \cdots c_K=0$`, we build confidence intervals as usual

`$$\widehat{C} \pm \text{critical value} \times \widehat{\mathsf{se}}(\widehat{C})$$`

Different methods provide control for FWER by modifying the **critical value**.

Assuming we care only about mean differences between experimental conditions

---
# FWER control in ANOVA

- **Tukey**'s honestly significant difference (HSD) method: to compare (all) pairwise differences between subgroups, based on the largest possible pairwise mean differences, with extensions for unbalanced samples.
- **Scheffé**'s method: applies to any contrast (properties depends on sample size `$n$` and number of groups `$K$`, not the number of test). Better than Bonferroni if `$m$` is large. Can be used for any design, but not powerful.
- **Dunnett**'s method: only for all pairwise contrasts relative to a specific baseline (control).

---
# Tukey's honest significant difference

Idea: controlling for the range 
`$$\max\{\mu_1, \ldots, \mu_K\} - \min\{\mu_1, \ldots \mu_K\}$$`
automatically controls FWER for other pairwise differences.

---

# Scheffé's criterion

.box-inv-6.sp-after[Control for **all** possible linear contrasts]
.center[
Critical value is `$\sqrt{(K-1)F}$`, 
where `$F$` is the `$(1-\alpha)$` quantile of the `$\mathsf{F}(K-1, n-K)$` distribution.

]

.box-inv-6.sp-after[Allows for data snooping (post-hoc hypothesis)]

.box-inv-6.sp-after[But not powerful...]

---
# Adjustment for one-way ANOVA

**Take home message**: 
 - same as usual, only with different **critical values**
 - larger cutoffs for `$p$`-values when procedure accounts for more tests

Everything is obtained using software.

---

# Numerical example

With `$K=5$` groups and `$n=9$` individuals per group (`arithmetic` example), critical value for two-sided test of zero difference with standardized `$t$`-test statistic and `$\alpha=5$`% are

- Scheffé's (all contrasts): 3.229
- Tukey's (all pairwise differences): 2.856 
- Dunnett's (difference to baseline): 2.543 
- unadjusted Student's `$t$`-distribution: 2.021

???

These were derived from the output of the function, sometimes by reverse-engineering.
`agricolae::scheffe.test`
`TukeyHSD`, `agricolae::HSD.test`
`DescTools::DunnettTest`
---
# Sometimes, there are too many tests...

---

# Scaling back expectations...

A simultaneous procedure that controls family-wise error rate (FWER) ensure any selected test has type I error `$\alpha$`.

With thousands of tests, this is too stringent a criterion.

The false discovery rate (FDR) provides a guarantee for the proportion **among selected** discoveries (tests for which we reject the null hypothesis).

Why use it? the false discovery rate is scalable:

- 2 type I errors out of 4 tests is unacceptable.
- 2 type I errors out of 100 tests is probably okay.

???

---

# False discovery rate

Suppose that `$m_0$` out of `$m$` null hypothesis are true

The **false discovery rate** is the proportion of false discovery among rejected nulls,

`$$\textsf{FDR} = \begin{cases} \frac{V}{R} & R > 0 \text{ (if one or more rejection)},\\ 0 & R=0 \text{ (if no rejection)}.\end{cases}$$`

???

False discovery rate offers weak-FWER control
 the property is only guaranteed under the scenario where all null hypotheses are true.

---

# Controlling false discovery rate

The Benjamini-Hochberg (1995) procedure for controlling false discovery rate is:

1. Order the _p_-values from the `$m$` tests from smallest to largest: `$p_{(1)} \leq \cdots \leq p_{(m)}$`
2. For level `$\alpha$` (e.g., `$\alpha=0.05$`), set 
`$$k=\max\left\{i: p_{(i)} \leq \frac{i}{m}\alpha\right\}$$`
3. Reject `$\mathscr{H}_{0(1)}, \ldots, \mathscr{H}_{0(k)}$`.

---

# Benjamini-Hochberg in a picture
.pull-left[
1. Plot _p_-values (_y_-axis) against their rank (_x_-axis)
   - .small[
   (the smallest _p_-value has rank `$1$`, the largest has rank `$m$`).
   ]
2. Draw the line `$y=\alpha/m x$`
  - .small[
  (zero intercept, slope `$\alpha/m$`)
  ]
3. Reject all null hypotheses associated to `$p$`-values located before the first time a point falls *above* the line.

]
.pull-right[

]

---

---
# Recap 1

- The test of equality of variance of the one-way ANOVA is seldom of interest (too general or vague)
- Rather, we care about specific comparisons (often linear contrasts)
- Must specify ahead of time which comparisons are of interest
    - otherwise it's easy to find something significant!
    - and multiplicity correction will be unfavorable.

---

# Recap 2

- Researchers often carry lots of hypothesis testing tests
   - the more you look, the more you find!
   - One of the many reasons for the replication crisis!
- Thus want to control probability of making a type I error (condemn innocent, incorrect finding) among all `$m$` tests performed
   - aka family-wise error rate (FWER)
   - Downside of multiplicity correction/adjustment is loss of power
   - upside is (more robust findings).

---

# Recap 3
   
ANOVA specific solutions (assuming equal variance, balanced large samples...)
   - Tukey's HSD (all pairwise differences), 
   - Dunnett's method (only differences relative to a reference category)
   - Scheffé's method (all potential linear contrasts)

Outside of ANOVA, some more general recipes:

- FWER: Bonferroni (suboptimal), Bonferroni-Holm (more powerful)
   - FDR: Benjamini-Hochberg

Pick the one that controls FWER, but penalizes less!

???

Example of the last point is comparison between Bonferroni and Scheffé: with large number of tests, the latter may be less stringent and lead to more discovery while having guarantees for the FWER