Multiway ANOVA and MANOVA

# Multiway ANOVA and MANOVA

**Session 7**

]
---
class: title title-1

# Outline

.box-6.large.sp-after-half[Multiway ANOVA]

.box-5.large.sp-after-half[MANOVA]

---

layout: false
name: factorial-designs
class: center middle section-title section-title-6 animated fadeIn

# Multifactorial designs

---
class: title title-6
# Beyond two factors

We can consider multiple factors `$A$`, `$B$`, `$C$`, `$\ldots$` with respectively `$n_a$`, `$n_b$`, `$n_c$`, `$\ldots$` levels and with `$n_r$` replications for each.

The total number of treatment combinations is

.box-inv-6.sp-after-half[
`$n_a \times n_b \times n_c \times \cdots$`
]

.box-6.medium[
**Curse of dimensionality**
]

---

Each cell of the cube is allowed to have a different mean

`$$\begin{align*}
\underset{\text{response}\vphantom{cell}}{Y_{ijkr}\vphantom{\mu_{j}}} = \underset{\text{cell mean}}{\mu_{ijk}} + \underset{\text{error}\vphantom{cell}}{\varepsilon_{ijkr}\vphantom{\mu_{j}}}
\end{align*}$$`
with `$\varepsilon_{ijkt}$` are independent error term for 
- row `$i$`
- column `$j$`
- depth `$k$`
- replication `$r$`

---
class: title title-6
# Parametrization of a three-way ANOVA model

With the **sum-to-zero** parametrization with factors `$A$`, `$B$` and `$C$`, write the response as

`$$\begin{align*}\underset{\text{theoretical average}}{\mathsf{E}(Y_{ijkr})} &= \quad \underset{\text{global mean}}{\mu} \\ &\quad +\underset{\text{main effects}}{\alpha_i + \beta_j + \gamma_k}  \\ & \quad + \underset{\text{two-way interactions}}{(\alpha\beta)_{ij} + (\alpha\gamma)_{ik} + (\beta\gamma)_{jk}} \\ & \quad + \underset{\text{three-way interaction}}{(\alpha\beta\gamma)_{ijk}}\end{align*}$$`

---

.small[
<div class="figure" style="text-align: center">
<img src="img/06/cube.png" alt="global mean, row, column and depth main effects" width="20%" /><img src="img/06/cube_rows.png" alt="global mean, row, column and depth main effects" width="20%" /><img src="img/06/cube_column.png" alt="global mean, row, column and depth main effects" width="20%" /><img src="img/06/cube_depth.png" alt="global mean, row, column and depth main effects" width="20%" />
<p class="caption">global mean, row, column and depth main effects</p>
</div>
]
.small[
<div class="figure" style="text-align: center">
<img src="img/06/cube_rowcol.png" alt="row/col, row/depth and col/depth interactions and three-way interaction." width="20%" /><img src="img/06/cube_rowdepth.png" alt="row/col, row/depth and col/depth interactions and three-way interaction." width="20%" /><img src="img/06/cube_coldepth.png" alt="row/col, row/depth and col/depth interactions and three-way interaction." width="20%" /><img src="img/06/cube_all.png" alt="row/col, row/depth and col/depth interactions and three-way interaction." width="20%" />
<p class="caption">row/col, row/depth and col/depth interactions and three-way interaction.</p>
</div>
]

---

---

# Example of three-way design

.small[
Petty, Cacioppo and Heesacker (1981). Effects of rhetorical questions on persuasion: A cognitive response analysis. Journal of Personality and Social Psychology.

A `$2 \times 2 \times 2$` factorial design with 8 treatments groups and `$n=160$` undergraduates.

Setup: should a comprehensive exam be administered to bachelor students in their final year?

- **Response** Likert scale on `$-5$` (do not agree at all) to `$5$` (completely agree)
- **Factors**
- `$A$`: strength of the argument (`strong` or `weak`)
- `$B$`: involvement of students `low` (far away, in a long time) or  `high` (next year, at their university)
- `$C$`: style of argument, either `regular` form or `rhetorical` (Don't you think?, ...)
]

---

# Interaction plot

.small[
Interaction plot for a  `$2 \times 2 \times 2$` factorial design from Petty, Cacioppo and Heesacker (1981)
]

???

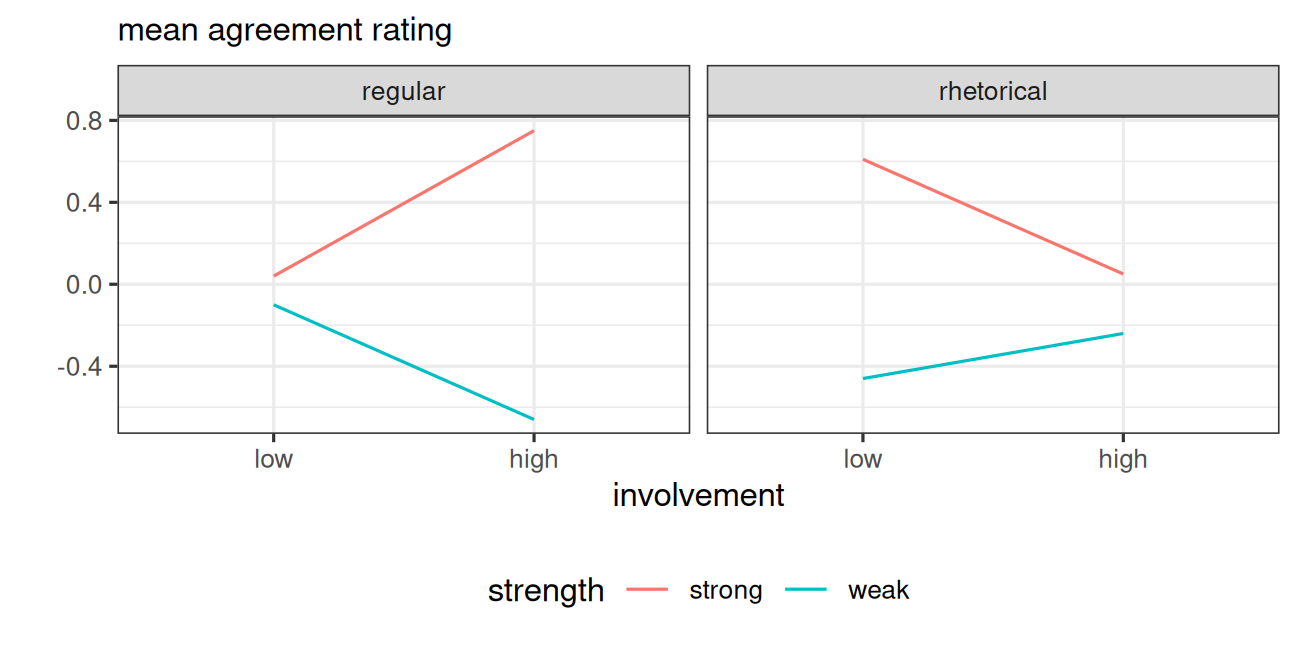
p.472 of Keppel and Wickens

---

#  The microwave popcorn experiment

What is the best brand of microwave popcorn?

- **Factors**
- brand (two national, one local)
- power: 500W and 600W
- time: 4, 4.5 and 5 minutes
- **Response**: <s>weight</s>, <s>volume</s>, <s>number</s>, percentage of popped kernels.
- Pilot study showed average of 70% overall popped kernels (10% standard dev), timing values reasonable
- Power calculation suggested at least `$r=4$` replicates, but researchers proceeded with `$r=2$`...

---

# ANOVA table

``` r
data(popcorn, package = 'hecedsm')
# Fit model with three-way interaction
model <- aov(percentage ~ brand*power*time,
             data = popcorn)
# ANOVA table - 'anova' is ONLY for balanced designs
anova_table <- anova(model) 
# Quantile-quantile plot
car::qqPlot(model)
```

Model assumptions: plots and tests are meaningless with `$n_r=2$` replications per group...

]

---

# Quantile-quantile plot

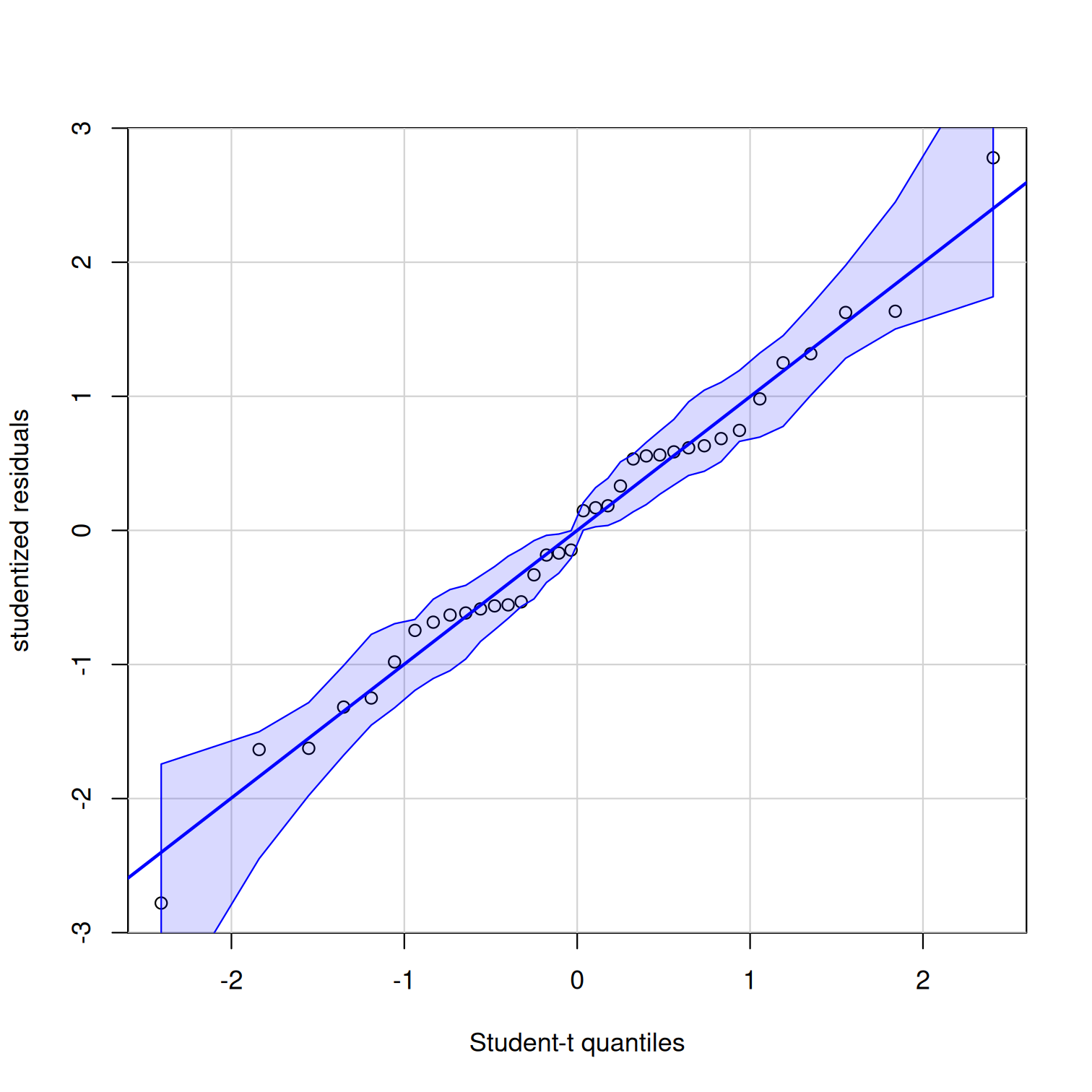
All points fall roughly on a straight line.

---

# Code for interaction plot

``` r
popcorn |> 
   group_by(brand, time, power) |>
   summarize(meanp = mean(percentage)) |>
ggplot(mapping = aes(x = power, 
                     y = meanp, 
                     col = time, 
                     group = time)) + 
  geom_line() + 
  facet_wrap(~brand)
```

---

# Interaction plot

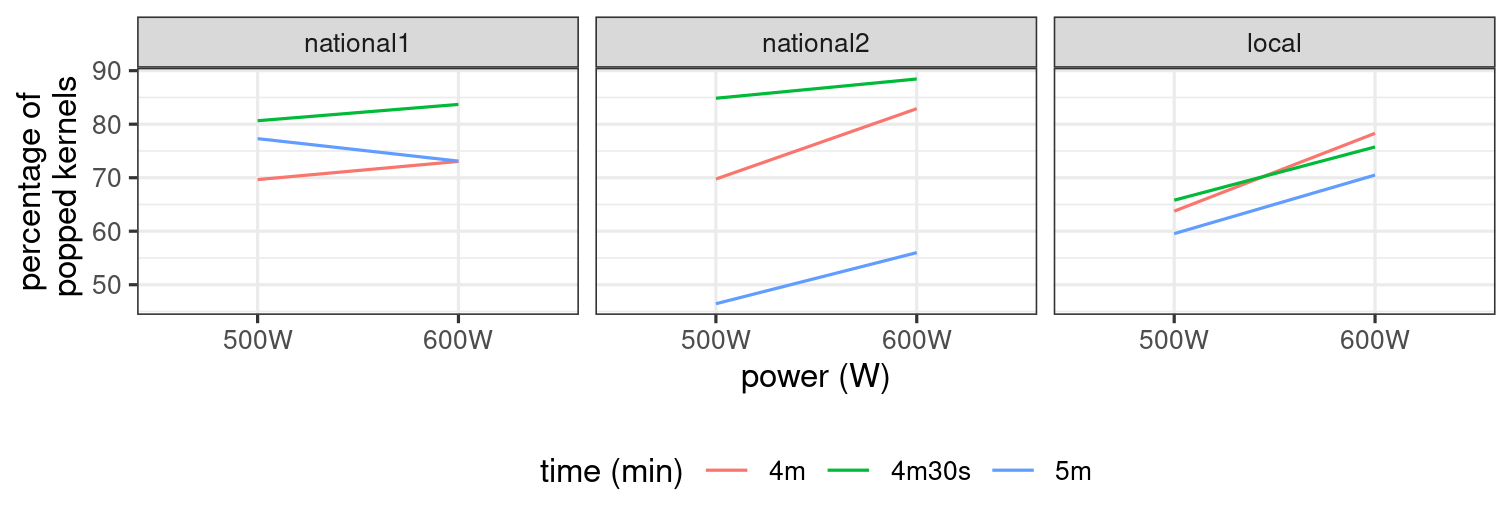
No evidence of three-way interaction (hard to tell with `$r=2$` replications).

---

# Variance decomposition for balanced designs

| terms | degrees of freedom | 
|:---:|:-----|:-------|
| `$A$` | `$n_a-1$` | 
| `$B$` | `$n_b-1$` | 
| `$C$` | `$n_c-1$` | 
| `$AB$` | `$(n_a-1)(n_b-1)$` | 
| `$AC$` | `$(n_a-1)(n_c-1)$` | 
| `$BC$` | `$(n_b-1)(n_c-1)$` | 
| `$ABC$` | `${\small (n_a-1)(n_b-1)(n_c-1)}$` | 
| `$\text{residual}$` | `$n_an_bn_c(R-1)$` | 
| `$\text{total}$` | `$n_an_bn_cn_r-1$` |

]

---

# Analysis of variance table for the 3-way model
<table class="table" style="margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:left;">   </th>
   <th style="text-align:right;"> Degrees of freedom </th>
   <th style="text-align:right;"> Sum of squares </th>
   <th style="text-align:right;"> Mean square </th>
   <th style="text-align:right;"> F statistic </th>
   <th style="text-align:right;"> p-value </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:left;"> brand </td>
   <td style="text-align:right;"> 2 </td>
   <td style="text-align:right;"> 331.10 </td>
   <td style="text-align:right;"> 165.55 </td>
   <td style="text-align:right;"> 1.89 </td>
   <td style="text-align:right;"> 0.180 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> power </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 455.11 </td>
   <td style="text-align:right;"> 455.11 </td>
   <td style="text-align:right;"> 5.19 </td>
   <td style="text-align:right;"> 0.035 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> time </td>
   <td style="text-align:right;"> 2 </td>
   <td style="text-align:right;"> 1554.58 </td>
   <td style="text-align:right;"> 777.29 </td>
   <td style="text-align:right;"> 8.87 </td>
   <td style="text-align:right;"> 0.002 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> brand:power </td>
   <td style="text-align:right;"> 2 </td>
   <td style="text-align:right;"> 196.04 </td>
   <td style="text-align:right;"> 98.02 </td>
   <td style="text-align:right;"> 1.12 </td>
   <td style="text-align:right;"> 0.349 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> brand:time </td>
   <td style="text-align:right;"> 4 </td>
   <td style="text-align:right;"> 1433.86 </td>
   <td style="text-align:right;"> 358.46 </td>
   <td style="text-align:right;"> 4.09 </td>
   <td style="text-align:right;"> 0.016 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> power:time </td>
   <td style="text-align:right;"> 2 </td>
   <td style="text-align:right;"> 47.71 </td>
   <td style="text-align:right;"> 23.85 </td>
   <td style="text-align:right;"> 0.27 </td>
   <td style="text-align:right;"> 0.765 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> brand:power:time </td>
   <td style="text-align:right;"> 4 </td>
   <td style="text-align:right;"> 47.33 </td>
   <td style="text-align:right;"> 11.83 </td>
   <td style="text-align:right;"> 0.13 </td>
   <td style="text-align:right;"> 0.967 </td>
  </tr>
  <tr>
   <td style="text-align:left;"> Residuals </td>
   <td style="text-align:right;"> 18 </td>
   <td style="text-align:right;"> 1577.87 </td>
   <td style="text-align:right;"> 87.66 </td>
   <td style="text-align:right;">  </td>
   <td style="text-align:right;">  </td>
  </tr>
</tbody>
</table>

---

# Omitting terms in a factorial design

The more levels and factors, the more parameters to estimate (and replications needed)
- Costly to get enough observations / power
- The assumption of normality becomes more critical when `$r=2$`!

It may be useful not to consider some interactions if they are known or (strongly) suspected not to be present

- If important interactions are omitted from the model, biased estimates/output!

---

# Guidelines for the interpretation of effects

Start with the most complicated term (bottom up)

- If the three-way interaction `$ABC$` is significative:
    - don't interpret main effects or two-way interactions!
    - comparison is done cell by cell within each level
- If the `$ABC$` term isn't significative:
    - can marginalize and interpret lower order terms
    - back to a series of two-way ANOVAs

---

# Marginalization vs main effects

**Marginalization** means that we reduce the dimension of the problem, e.g., we transform a three-way ANOVA into a two-way ANOVA by collapsing over a dimension.

**Main effects** are the effects of factors `$A$`, `$B$`, `$C$` (i.e., row, column and depth effects).

---

# What contrasts are of interest?

- Can view a three-way ANOVA as a series of one-way ANOVA or two-way ANOVA...

Depending on the goal and if the interactions are significative or not, could compare for variable `$A$`
- marginal contrast `$\psi_A$` (averaging over `$B$` and `$C$`)
- marginal conditional contrast for particular subgroup: `$\psi_A$` within `$c_1$`
- contrast involving two variables: `$\psi_{AB}$`
- contrast differences between treatment at `$\psi_A \times B$`, averaging over `$C$`.
- etc.

See helper code and chapter 22 of Keppel & Wickens (2004) for a detailed example.

---

# Effects and contrasts for microwave-popcorn

Following preplanned comparisons

- Which combo (brand, power, time) gives highest popping rate? (pairwise comparisons of all combos)
- Best brand overall (marginal means marginalizing over power and time, assuming no interaction)
- Effect of time and power on percentage of popped kernels 
- pairwise comparison of time `$\times$` power
- main effect of power
- main effect of time

---

# Preplanned comparisons using `emmeans`

Let `$A$`=brand, `$B$`=power, `$C$`=time

Compare difference between percentage of popped kernels for 4.5 versus 5 minutes, for brands 1 and 2

`$$\mathscr{H}_0: (\mu_{1.2} -\mu_{1.3}) - (\mu_{2.2} - \mu_{2.3}) = 0$$`

``` r
library(emmeans)
# marginal means
emm_popcorn_AC <- emmeans(model, 
                          specs = c("brand","time"))
contrast_list <- 
  list(
    brand12with4.5vs5min = c(0, 0, 0, 1, -1, 0, -1, 1,0))
contrast(emm_popcorn_AC,  # marginal mean (no time)
         method = contrast_list) # list of contrasts
```

]

---

# Preplanned comparisons

Compare all three times (4, 4.5 and 5 minutes)

At level 99% with Tukey's HSD method

- Careful! Potentially misleading because there is a `brand * time` interaction present.

``` r
# List of variables to keep go in `specs`: keep only time
emm_popcorn_C <- emmeans(model, specs = "time")
pairs(emm_popcorn_C, 
      adjust = "tukey", 
      level = 0.99, 
      infer = TRUE)
```

---

# Multivariate analysis of variance

---

---

# Motivational example

From Anandarajan et al. (2002), Canadian Accounting Perspective

> This study questions whether the current or proposed Canadian standard of disclosing a going-concern contingency is viewed as equivalent to the standard adopted in the United States by financial statement users. We examined loan officers’ perceptions across three different formats

---

# Alternative going-concern reporting formats

Bank loan officers were selected as the appropriate financial statement users for this study.

Experiment was conducted on the user’s interpretation of a
going-concern contingency when it is provided in one of three
disclosure formats:

1. Integrated note (Canadian standard)
2. Stand-alone note (Proposed standard)
3. Stand-alone note plus modified report with explanatory
paragraph (standard adopted in US and other countries)

---
# Multivariate response

![](img/13/questionnaire.png)

---

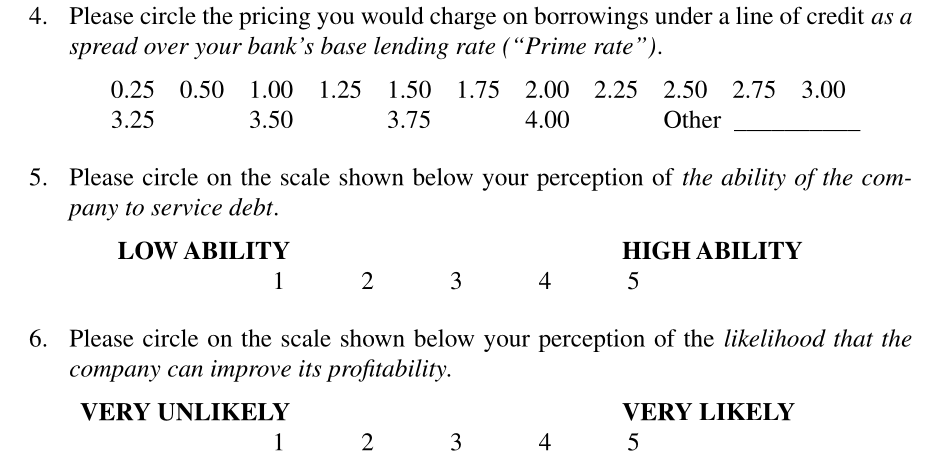
# Why use MANOVA?

1. Control experimentwise error
  - do a single test instead of `$J$` univariate ANOVAs, thereby reducing the type I error
2. Detect differences in combination that would not be found with univariate tests
3. Increase power (context dependent)

---

# Multivariate model
Postulate the following model:
`$$\boldsymbol{Y}_{ij} \sim \mathsf{Normal}_p(\boldsymbol{\mu}_j, \boldsymbol{\Sigma}), \qquad j = 1, \ldots J$$`

Each response `$\boldsymbol{Y}_{ij}$` is `$p$`-dimensional.

We assume multivariate measurements are independent of one another, with

- the same multivariate normal distribution
- same covariance matrix `$\boldsymbol{\Sigma}$` (each measurement can have different variance)
- same mean vector `$\boldsymbol{\mu}_j$`  within each `$j=1, \ldots, J$` experimental groups.

]

The model is fitted using multivariate linear regression.

---
# Model fitting with multivariate response

In **R**, we fit a model binding the different vectors of response in a matrix with `$p$` columns

``` r
data(AVC02, package = "hecedsm")
# Fit the model binding variables with cbind
# on left of tilde (~) symbol
modMANOVA <- manova(
  cbind(prime, debt, profitability) ~ format, 
  data = AVC02)
```

---

# Bivariate MANOVA

.pull-left[
<img src="img/09/fig8.png" width="100%" style="display: block; margin: auto;" />
]
.pull-right[
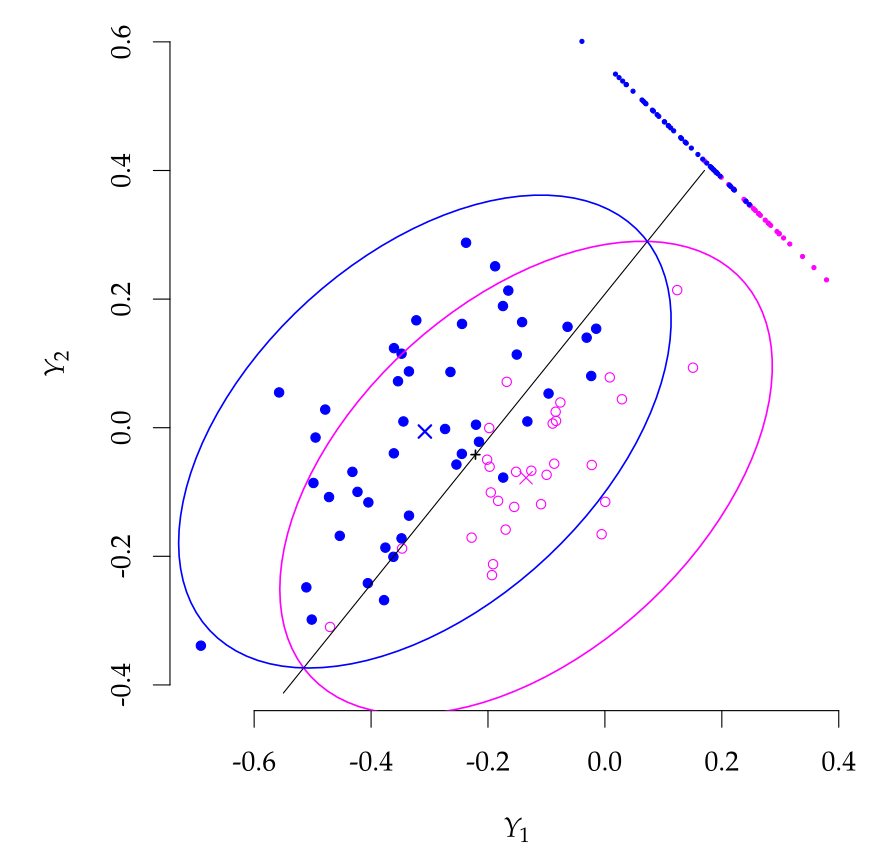
Confidence ellipses for bivariate MANOVA with discriminant analysis.

We use the correlation between the `$p$` measurements to find better discriminant 
(the diagonal line is the best separating plane between the two variables).

]

---

# Confidence intervals and confidence regions

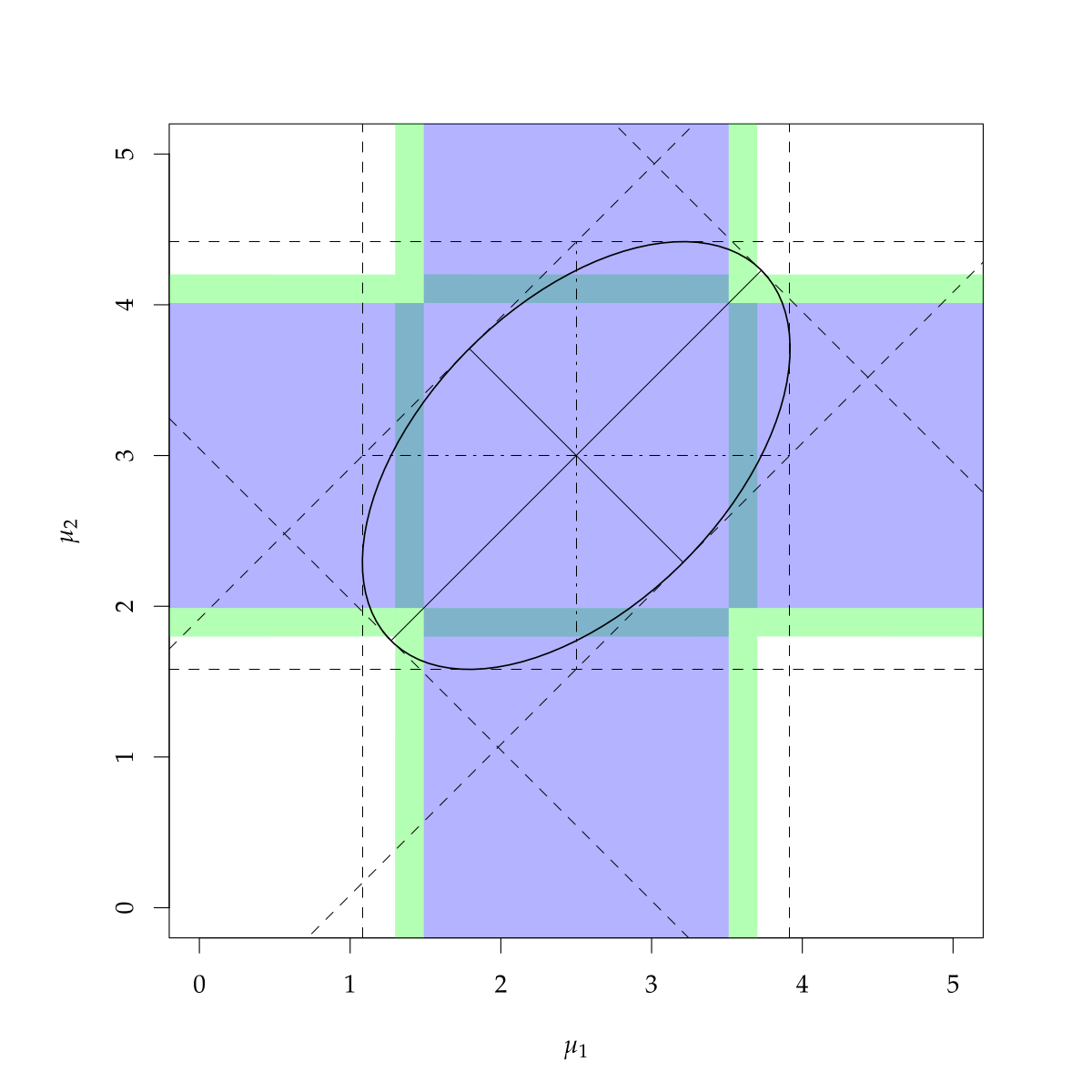
<img src="img/09/fig5.png" width="100%" style="display: block; margin: auto;" />
]

.pull-right[
Simultaneous confidence region (ellipse), marginal confidence intervals (blue) and Bonferroni-adjusted intervals (green).

The dashed lines show the univariate projections of the confidence ellipse.
]

---
# Model assumptions

Same as ANOVA, with in addition

- The response follow a multivariate normal distribution 
  - Shapiro–Wilk test, univariate Q-Q plots 
- The covariance matrix is the same for all subjects
  - Box's `$M$` test is often used, but highly sensitive to departures from the null (other assumptions impact the test)

Normality matters more in small samples (but tests will often lead to rejection, notably because of rounded measurements or Likert scales)

]
---
# When to use MANOVA?

In addition, for this model to make sense, you need just enough correlation (Goldilock principle)

- if correlation is weak, use univariate analyses 
   - (no gain from multivariate approach relative to one-way ANOVAs)
   - less power due to additional covariance parameter estimation
 - if correlation is too strong, redundancy
    - don't use Likert scales that measure a similar dimension (rather, consider PLS or factor analysis)

---
# Testing equality of mean vectors

The null hypothesis is that the `$J$` groups have the same mean

- `$\mathscr{H}_0: \boldsymbol{\mu}_1 = \cdots = \boldsymbol{\mu}_J$` against the alternative that at least one vector is different from the rest.

- The null imposes `$(J-1) \times p$` restrictions on the parameters.

The test statistic is Hotelling's `$T^2$` (with associated null distribution), but we can compute using an `$\mathsf{F}$` distribution.

---
# Choice of test statistic

In higher dimensions, with `$J \geq 3$`, there are many statistics that can be used to test equality of mean.

The statistics are constructed from within/between sum covariance matrices.

These are

- Roy's largest root (most powerful provided all assumptions hold)
- Wilk's `$\Lambda$`: most powerful, most commonly used
- **Pillai's trace**: most robust choice for departures from normality or equality of covariance matrices

Most give similar conclusion, and they are all equivalent with `$J=2$`.

---

# Results for MANOVA

``` r
summary(modMANOVA) # Pilai is default
```

```
##            Df  Pillai approx F num Df den Df Pr(>F)
## format      2 0.02581  0.55782      6    256 0.7637
## Residuals 129
```

``` r
summary(modMANOVA, test = "Wilks")
```

```
##            Df   Wilks approx F num Df den Df Pr(>F)
## format      2 0.97424   0.5561      6    254  0.765
## Residuals 129
```

``` r
summary(modMANOVA, test = "Hotelling-Lawley")
```

```
##            Df Hotelling-Lawley approx F num Df den Df Pr(>F)
## format      2         0.026397  0.55434      6    252 0.7664
## Residuals 129
```

``` r
summary(modMANOVA, test = "Roy") # not reliable here?
```

```
##            Df      Roy approx F num Df den Df Pr(>F)
## format      2 0.024436   1.0426      3    128 0.3761
## Residuals 129
```

]
---

# MANOVA for repeated measures

We can also use MANOVA for repeated measures to get  away from the hypothesis of equal variance per group or equal correlation.

``` r
model <- afex::aov_ez(
  id = "id",           # subject id
  dv = "latency",      # response
  within = "stimulus", # within-subject
  data = hecedsm::AA21,
  fun_aggregate = mean)
model$Anova # for models fitted via 'afex'
```

---
# Output

```
## 
## Type III Repeated Measures MANOVA Tests: Pillai test statistic
##             Df test stat approx F num Df den Df    Pr(>F)    
## (Intercept)  1   0.95592   238.56      1     11 8.373e-09 ***
## stimulus     1   0.09419     0.52      2     10    0.6098    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

Less powerful than repeated measures ANOVA because we have to estimate more parameters. Still assumes that the covariance structure is the same for each experimental group.

]

---

# Follow-up analyses

Researchers often conduct *post hoc* univariate tests using univariate ANOVA. In **R**, Holm-Bonferonni's method is applied for marginal tests (you need to correct for multiple testing!)

``` r
# Results for univariate analysis of variance (as follow-up)
summary.aov(modMANOVA)
# Note the "rep.meas" as default name 
# to get means of each variable separately
emmeans::emmeans(modMANOVA, specs = c("format", "rep.meas"))
```

A better option is to proceed with descriptive discriminant analysis, a method that tries to find the linear combinations of the vector means to discriminate between groups. Beyond the scope of the course.

]