Analysis of covariance and moderation
Session 8
MATH 80667A: Experimental Design and Statistical Methods
HEC Montréal
Analysis of covariance
Covariates
Covariate Explanatory measured before the experiment
Typically, cannot be acted upon.
Example
socioeconomic variables
environmental conditions
IJLR: It's Just a Linear Regression...
All ANOVA models covered so far are linear regression model.
The latter says that
E(Yiβp)average responsel=β0+β1X1i+⋯+βpXpilinear (i.e., additive) combination of explanatories
In an ANOVA, the model matrix X simply includes columns with −1, 0 and 1 for group indicators that enforce sum-to-zero constraints.
What's in a model?
In experimental designs, the explanatories are
- experimental factors (categorical)
- continuous (dose-response)
Random assignment implies
no systematic difference between groups.
ANCOVA = Analysis of covariance
- Analysis of variance with added continuous covariate(s) to reduce experimental error (similar to blocking).
- These continuous covariates are typically concomitant variables (measured alongside response).
- Including them in the mean response (as slopes) can help reduce the experimental error (residual error).
Control to gain power!
Identify external sources of variations
- enhance balance of design (randomization)
- reduce mean squared error of residuals to increase power
These steps should in principle increase power if the variables used as control are correlated with the response.
Example
Abstract of van Stekelenburg et al. (2021)
In three experiments with more than 1,500 U.S. adults who held false beliefs, participants first learned the value of scientific consensus and how to identify it. Subsequently, they read a news article with information about a scientific consensus opposing their beliefs. We found strong evidence that in the domain of genetically engineered food, this two-step communication strategy was more successful in correcting misperceptions than merely communicating scientific consensus.
Aart van Stekelenburg, Gabi Schaap, Harm Veling and Moniek Buijzen (2021), Boosting Understanding and Identification of Scientific Consensus Can Help to Correct False Beliefs, Psychological Science https://doi.org/10.1177/09567976211007788
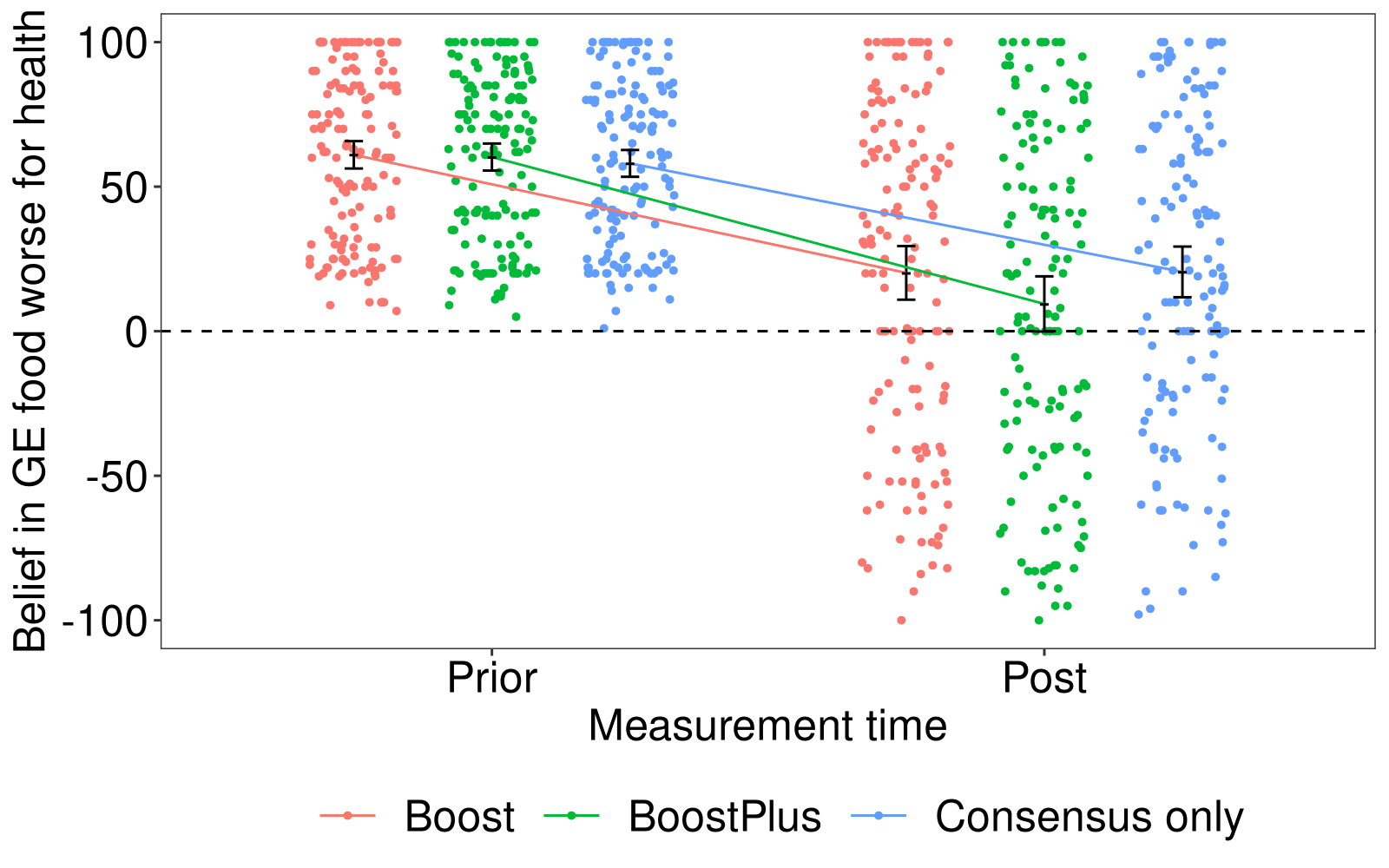
Experiment 2: Genetically Engineered Food
We focus on a single experiment; preregistered exclusion criteria led to n=442 total sample size (unbalanced design).
Three experimental conditions:
Boost Boost Plus Consensus only (consensus)
Model formulation
Use post as response variable and prior beliefs as a control variable in the analysis of covariance.
their response was measured on a visual analogue scale ranging from –100 (I am 100% certain this is false) to 100 (I am 100% certain this is true) with 0 (I don’t know) in the middle.
Plot of post vs prior response
Model formulation
Average for the rth replication of the ith experimental group is E(postir)=μ+αiconditioni+βpriorir.Va(postir)=σ2
We assume that there is no interaction between condition and prior
- the slopes for
priorare the same for eachconditiongroup. - the effect of prior is linear
Contrasts of interest
- Difference between average boosts (
BoostandBoostPlus) and control (consensus) - Difference between
BoostandBoostPlus(pairwise)
Inclusion of the prior score leads to increased precision for the mean (reduces variability).
Contrasts with ANCOVA
- The estimated marginal means will be based on a fixed value of the covariate (rather than detrended values)
- In the
emmeanspackage, the average of the covariate is used as value. - the difference between levels of
conditionare the same for any value ofprior(parallel lines), but the uncertainty changes.
Multiple testing adjustments:
- Methods of Bonferroni (prespecified number of tests) and Scheffé (arbitrary contrasts) still apply
- Can't use Tukey anymore (adjusted means are not independent anymore).
Data analysis - loading data
library(emmeans)options(contrasts = c("contr.sum", "contr.poly"))data(SSVB21_S2, package = "hecedsm")# Check balancewith(SSVB21_S2, table(condition))## condition## Boost BoostPlus consensus ## 149 147 146Data analysis - scatterplot
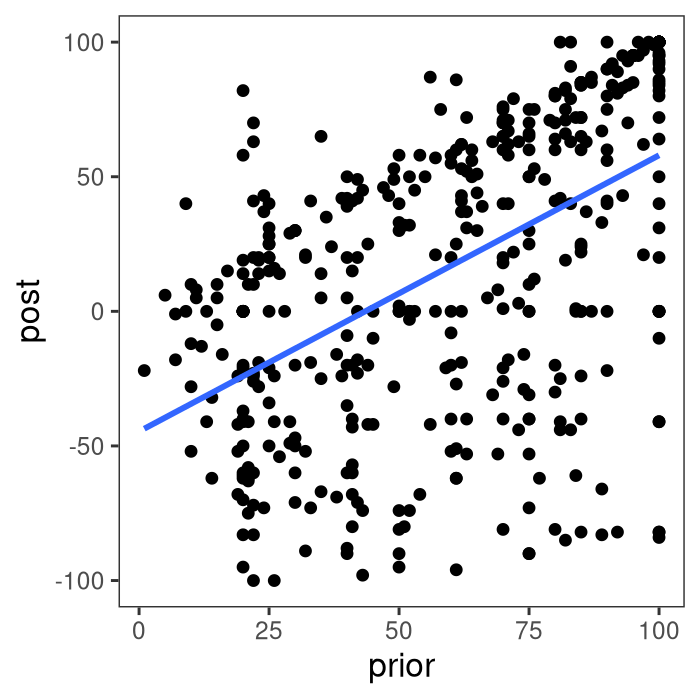
library(ggplot2)ggplot(data = SSVB21_S2, aes(x = prior, y = post)) + geom_point() + geom_smooth(method = "lm", se = FALSE)Strong correlation; note responses that achieve max of scale.
Data analysis - model
# Check that the data are well randomizedcar::Anova(lm(prior ~ condition, data = SSVB21_S2), type = 2)# Fit linear model with continuous covariatemodel1 <- lm(post ~ condition + prior, data = SSVB21_S2)# Fit model without for comparisonmodel2 <- lm(post ~ condition, data = SSVB21_S2)# Global test for differencescar::Anova(model1)car::Anova(model2)Data analysis - ANOVA table
| term | sum of squares | df | statistic | p-value |
|---|---|---|---|---|
| condition | 14107 | 2 | 3.0 | 0.05 |
| prior | 385385 | 1 | 166.1 | 0.00 |
| Residuals | 1016461 | 438 |
| term | sum of squares | df | statistic | p-value |
|---|---|---|---|---|
| condition | 11680 | 2 | 1.83 | 0.162 |
| Residuals | 1401846 | 439 |
Data analysis - contrasts
emm1 <- emmeans(model1, specs = "condition")# Note order: Boost, BoostPlus, consensusemm2 <- emmeans(model2, specs = "condition")# Not comparable: since one is detrended and the other isn'tcontrast_list <- list( "boost vs control" = c(0.5, 0.5, -1), #av. boosts vs consensus "Boost vs BoostPlus" = c(1, -1, 0))contrast(emm1, method = contrast_list, p.adjust = "holm")Data analysis - t-tests
| contrast | estimate | se | df | t stat | p-value |
|---|---|---|---|---|---|
| boost vs control | -8.37 | 4.88 | 438 | -1.72 | 0.09 |
| Boost vs BoostPlus | 9.95 | 5.60 | 438 | 1.78 | 0.08 |
prior (Holm-Bonferroni adjustment with k=2 tests)
| contrast | estimate | se | df | t stat | p-value |
|---|---|---|---|---|---|
| boost vs control | -5.71 | 5.71 | 439 | -1.00 | 0.32 |
| Boost vs BoostPlus | 10.74 | 6.57 | 439 | 1.63 | 0.10 |
Data analysis - assumption checks
# Test equality of variancelevene <- car::leveneTest( resid(model1) ~ condition, data = SSVB21_S2, center = 'mean')# Equality of slopes (interaction)car::Anova(lm(post ~ condition * prior, data = SSVB21_S2), model1, type = 2)Levene's test of equality of variance: F (2, 439) = 2.04 with a p-value of 0.131.
| term | sum of squares | df | statistic | p-value |
|---|---|---|---|---|
| condition | 14107 | 2 | 3.0 | 0.05 |
| prior | 385385 | 1 | 166.1 | 0.00 |
| condition:prior | 3257 | 2 | 0.7 | 0.50 |
| Residuals | 1016461 | 438 |
Model with interaction condition*prior. Slopes don't differ between condition.
The kitchen sink approach
Should we control for more stuff?
NO! ANCOVA is a design to reduce error
- Randomization should ensure that there is no confounding
- No difference (on average) between group given a value of the covariate.
- If it isn't the case, adjustment matters
Equal trends
- If trends are different, meaningful comparisons (?)
- Differences between groups depend on value of the covariate
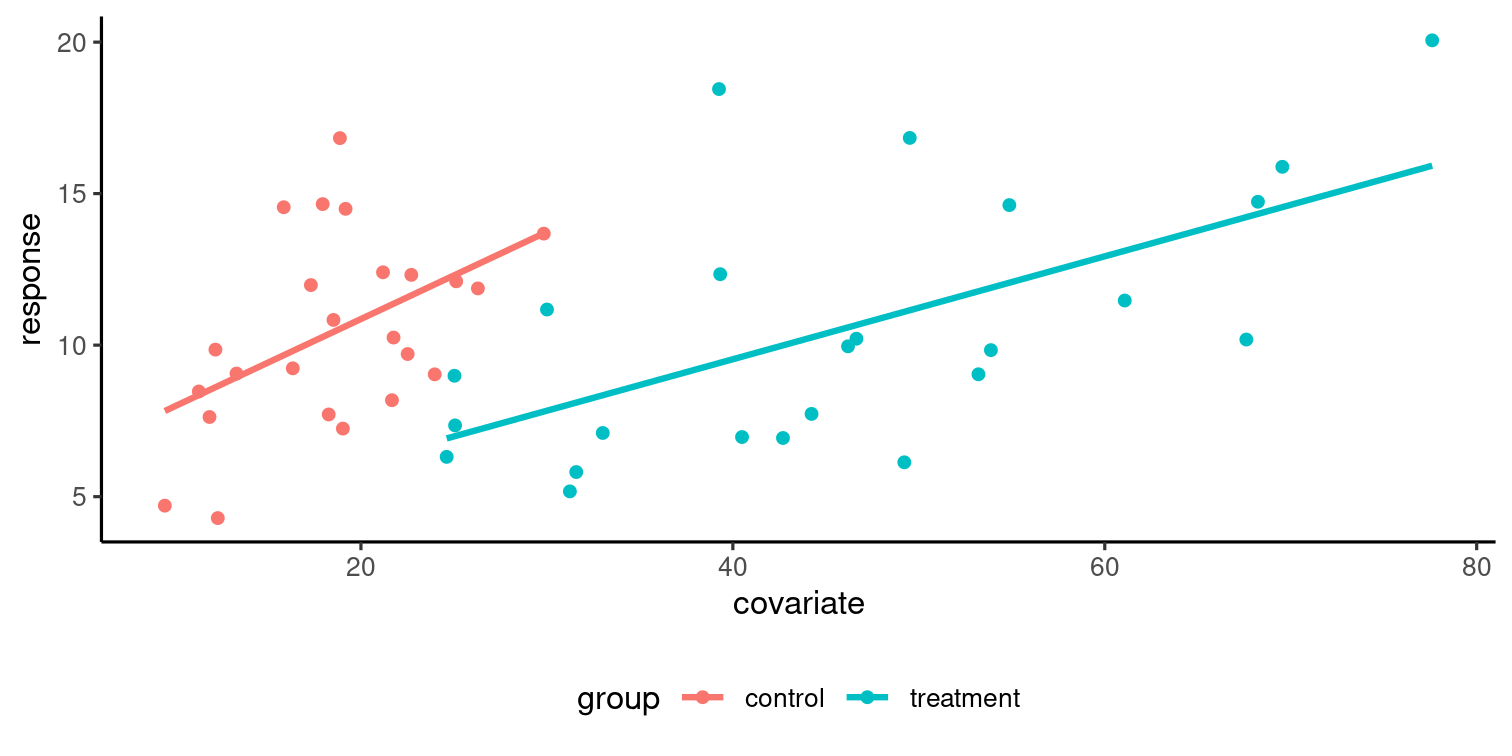 Due to lack of overlap, comparisons hazardous as they entail extrapolation one way or another.
Due to lack of overlap, comparisons hazardous as they entail extrapolation one way or another.Testing equal slope
Compare two nested models
- Null H0: model with covariate
- Alternative Ha: model with interaction covariate * experimental factor
Use anova to compare the models in R.
Moderation
Moderator
A moderator W modifies the direction or strength of the effect of an explanatory variable X on a response Y (interaction term).
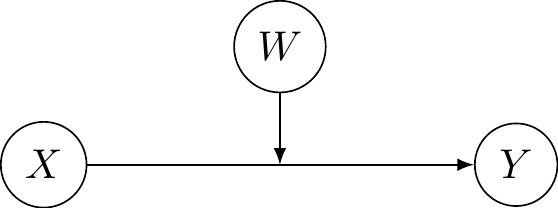
Directed acyclic graph of moderation
Interactions are not limited to experimental factors: we can also have interactions with confounders, explanatories, mediators, etc.
Moderation in a linear regression model
In a regression model, we simply include an interaction term to the model between W and X.
For example, if X is categorical with K levels and W is binary or continuous, imposing sum-to-zero constraints for α1,…,αK and β1,…,βK gives E(Y∣X=k,W=w)average response of group k at w=α0+αkintercept of group k+(β0+βk)slope of group kw
Testing for the interaction
Test jointly whether coefficients associated to XW are zero, i.e., β1=⋯=βK=0.
The moderator W can be continuous or categorical with L≥2 levels
The degrees of freedom (additional parameters for the interaction) in the F test are
- K−1 for continuous W
- are slopes parallel?
- (K−1)×(L−1) for categorical W
- are all subgroup averages the same?
Example
We consider data from Garcia et al. (2010), a study on gender discrimination. Participants were given a fictional file where a women was turned down promotion in favour of male colleague despite her being clearly more experimented and qualified.
The authors manipulated the decision of the participant, with choices:
- not to challenge the decision (no protest),
- a request to reconsider based on individual qualities of the applicants (individual)
- a request to reconsider based on abilities of women (collective).
sexism, which assesses pervasiveness of gender discrimination.Model fit
We fit the linear model with the interaction.
data(GSBE10, package = "hecedsm")lin_moder <- lm(respeval ~ protest*sexism, data = GSBE10)summary(lin_moder) # coefficientscar::Anova(lin_moder, type = 2) # testsANOVA table
| term | sum of squares | df | stat | p-value |
|---|---|---|---|---|
| sexism | 0.27 | 1 | 0.21 | .648 |
| protest:sexism | 12.49 | 2 | 4.82 | .010 |
| Residuals | 159.22 | 123 |
Effects
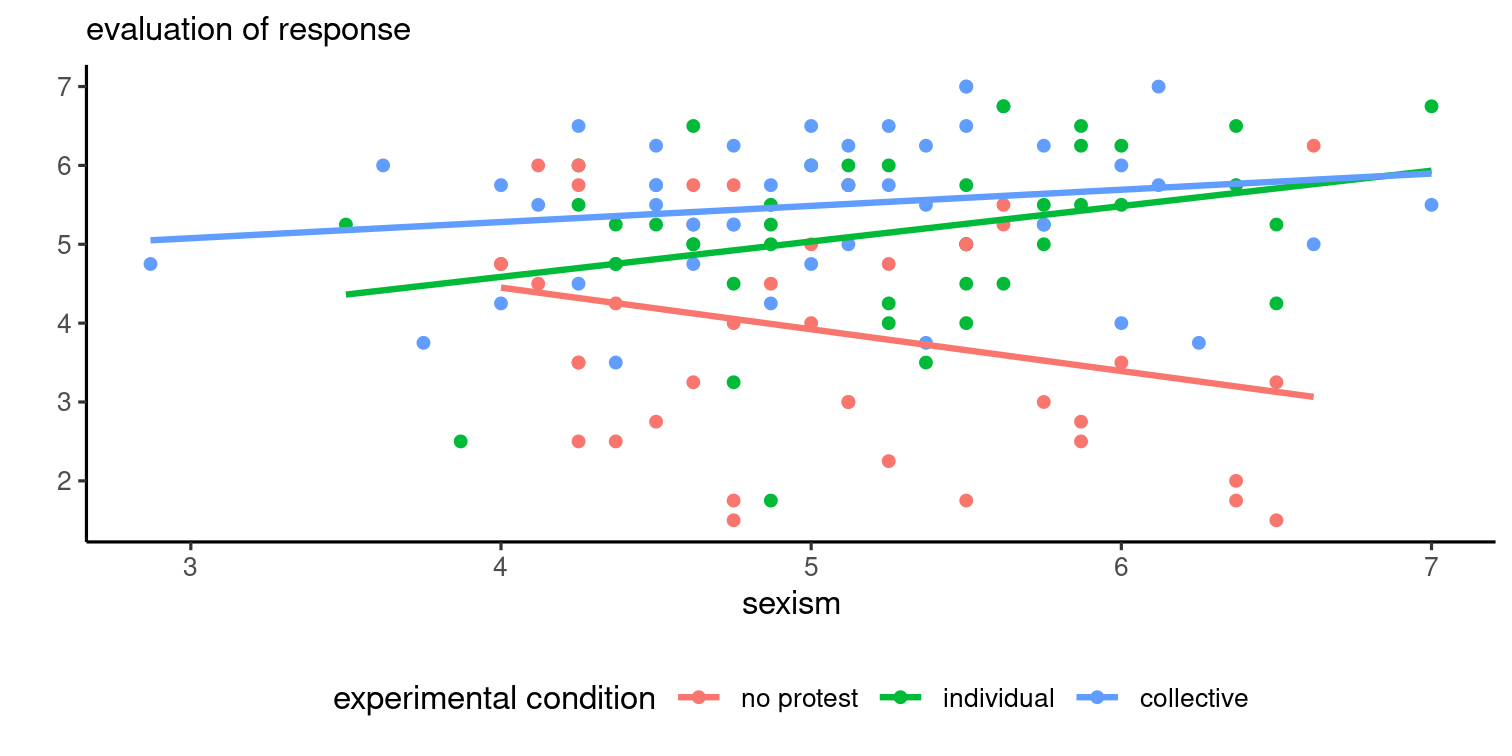
Results won't necessarily be reliable outside of the range of observed values of sexism.
Comparisons between groups
Simple effects and comparisons must be done for a fixed value of sexism (since the slopes are not parallel).
The default value in emmeans is the mean value of sexism, but we could query for averages at different values of sexism (below for empirical quartiles).
quart <- quantile(GSBE10$sexism, probs = c(0.25, 0.5, 0.75))emmeans(lin_moder, specs = "protest", by = "sexism", at = list("sexism" = quart))With moderating factors, give weights to each sub-mean corresponding to the frequency of the moderator rather than equal-weight to each category (weights = "prop").
Sensitivity analysis
The Johnson and Neyman (1936) method looks at the range of values of moderator W for which difference between treatments (binary X) is not statistically significant.
lin_moder2 <- lm( respeval ~ protest*sexism, data = GSBE10 |> # We dichotomize the manipulation, pooling protests together dplyr::mutate(protest = as.integer(protest != "no protest")))# Test for equality of slopes/intercept for two protest groupsanova(lin_moder, lin_moder2)# p-value of 0.18: fail to reject individual = collective.Syntax for plot
jn <- interactions::johnson_neyman( model = lin_moder2, # linear model pred = protest, # binary experimental factor modx = sexism, # moderator control.fdr = TRUE, # control for false discovery rate mod.range = range(GSBE10$sexism)) # range of values for sexismjn$plotPlot of Johnson−Neyman intervals
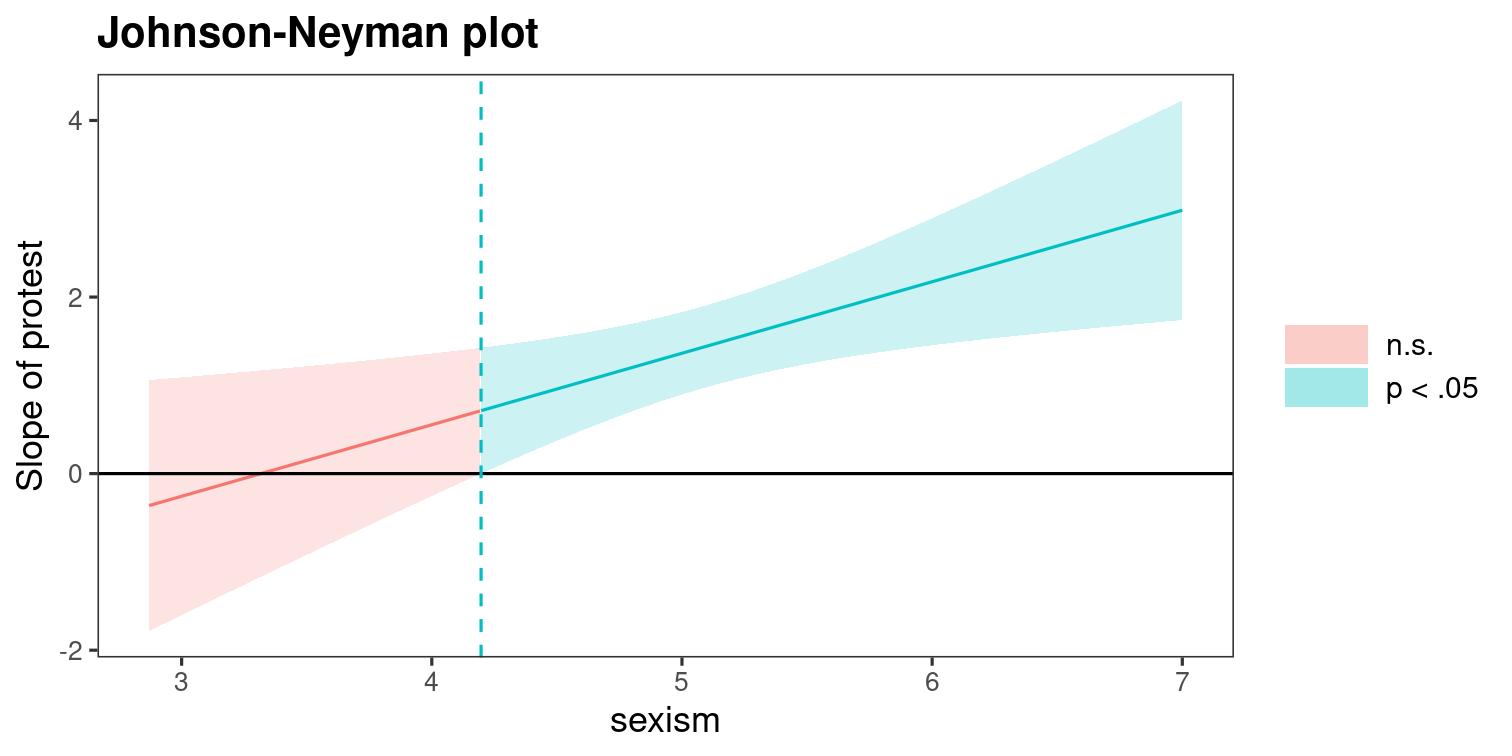
Johnson−Neyman plot for difference between protest and no protest as a function of sexism.
Moderation
More generally, moderation refers to any explanatory variable (whether continuous or categorical) which interacts with the experimental manipulation.
- For categorical-categorical, this is a multiway ANOVA model
- For continuous-categorical, use linear regression
Summary
- Inclusion of continuous covariates may help filtering out unwanted variability.
- These are typically variables measured before or alongside the response variable.
- This design reduce the residual error, leading to an increase in power (more ability to detect differences in average between experimental conditions).
- We are only interested in differences due to experimental condition (marginal effects).
- In general, there should be no interaction between covariates/blocking factors and experimental conditions.
- This hypothesis can be assessed by comparing the models with and without interaction, if there are enough units (e.g., equality of slope for ANCOVA).
- Moderators are variables that interact with the experimental factor. We assess their presence by testing for an interaction in a linear regression model.