Effect size and power

# Effect size and power

**Session 9**

]

---

# Outline
--

.box-1.large.sp-after-half[Effect sizes]

.box-3.large.sp-after-half[Power]

---
layout: false
name: effect
class: center middle section-title section-title-1 animated fadeIn

# Effect size

---
layout: true
class: title title-1

---

# Motivating example

Quote from the OSC psychology replication

> The key statistics provided in the paper to test the “depletion” hypothesis is the main effect of a one-way ANOVA with three experimental conditions and confirmatory information processing as the dependent variable; `$F(2, 82) = 4.05$`, `$p = 0.02$`, `$\eta^2 = 0.09$`. Considering the original effect size and an alpha of `$0.05$` the sample size needed to achieve `$90$`% power is `$132$` subjects.

.small[
Replication report of Fischer, Greitemeyer, and Frey (2008, JPSP, Study 2) by E.M. Galliani
]

---

# Translating statement into science

.box-inv-1.medium.sp-after-half[Q: How many observations should <br>I gather to reliably detect an effect?]
.box-inv-1.medium.sp-after-half[Q: How big is this effect?]

---

# Does it matter?

With large enough sample size, **any** sized difference between treatments becomes statistically significant.

.box-inv-1.medium.sp-before-half[
Statistical significance `$\neq$` practical relevance
]

But whether this is important depends on the scientific question.

---

# Example

- What is the minimum difference between two treatments that would be large enough to justify commercialization of a drug?
- Tradeoff between efficacy of new treatment vs status quo, cost of drug, etc.

---

# Using statistics to measure effects

Statistics and `$p$`-values are not good summaries of magnitude of an effect:

- the larger the sample size, the bigger the statistic, the smaller the `$p$`-value

Instead use

.pull-left[
.box-inv-1[standardized differences]
]
.pull-right[
.box-inv-1[percentage of variability explained]
]

Estimators popularized in the handbook
> Cohen, Jacob. Statistical Power Analysis for the Behavioral Sciences, 2nd ed., Routhledge, 1988.

---

# Illustrating effect size (differences)

.tiny[
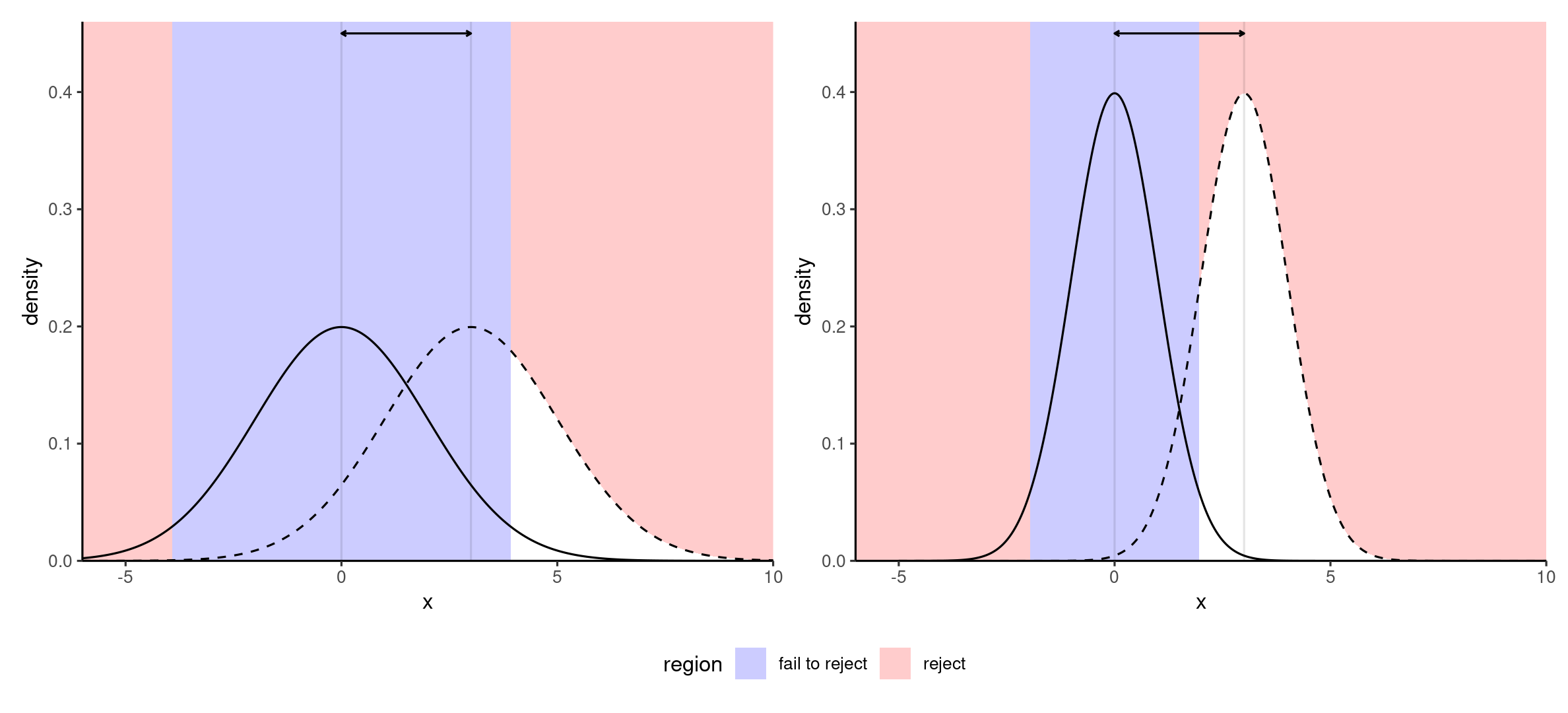
The plot shows null (thick) and true sampling distributions (dashed) for the same difference in sample mean with small (left) and large (right) samples.
]
---

# Estimands, estimators, estimates

- `$\mu_i$` is the (unknown) population mean of group `$i$` (parameter, or estimand)
- `$\widehat{\mu}_i$` is a formula (an estimator) that takes data as input and returns a numerical value (an estimate).
- throughout, use hats to denote estimated quantities:

.pull-left-3[
<img src="img/08/estimand.jpg" width="90%" style="display: block; margin: auto;" />
]
.pull-middle-3[
<img src="img/08/estimator.jpg" width="90%" style="display: block; margin: auto;" />
]

.tiny[
Left to right: parameter `$\mu$` (target), estimator `$\widehat{\mu}$` (recipe) and estimate `$\widehat{\mu}=10$` (numerical value, proxy)
]

???

From Twitter, @simongrund89

---

# Cohen's _d_

Standardized measure of effect (dimensionless=no units):

Assuming equal variance `$\sigma^2$`, compare mean of two groups `$i$` and `$j$`:

$$
d = \frac{\mu_i - \mu_j}{\sigma}
$$

- Usual estimator of Cohen's `$d$`, `$\widehat{d}=(\widehat{\mu}_i - \widehat{\mu}_j)/\widehat{\sigma}$`, uses sample average of groups and the square root of the pooled variance.

Cohen's classification: small (_d=0.2_), medium (_d=0.5_) or large (_d=0.8_) effect size.

Note: this is not the `$t$`-statistic (the denominator is the estimated standard deviation, not the standard error of the mean).

]
???

Note that there are multiple versions of Cohen's coefficients. 
These are the effects of the pwr package.
The small/medium/large effect size varies depending on the test! See the vignette of pwr for defaults.

---

# Effect size: ratio of variance

For a one-way ANOVA (equal variance `$\sigma^2$`) with more than two groups, Cohen's _f_ is the square root of

$$
f^2 = \frac{1}{\sigma^2} \sum_{j=1}^k \frac{n_j}{n}(\mu_j - \mu)^2,
$$
a weighted sum of squared difference relative to the overall mean `$\mu$`.

For `$k=2$` groups, Cohen's `$f$` and Cohen's `$d$` are related via `$f=d/2$`.

---

# Effect size: proportion of variance

If there is a single experimental factor `$A$`, we break down the variability as `$$\sigma^2_{\text{total}} = \sigma^2_{\text{resid}} + \sigma^2_{\text{A}}$$` and define the percentage of variability explained by the effect of `$A$` as.
`$$\eta^2 = \frac{\text{explained variability}}{\text{total variability}}= \frac{\sigma^2_{A}}{\sigma^2_{\text{total}}}.$$`
 
---

# Coefficient of determination estimator

For the balanced one-way between-subject ANOVA, typical estimator is the **coefficient of determination**

$$
\widehat{\eta}^2 \equiv \widehat{R}{}^2 = \frac{F\nu_1}{F\nu_1 + \nu_2}
$$
where `$\nu_1 = K-1$` and `$\nu_2 = n-K$` are the degrees of freedom for the one-way ANOVA with `$n$` observations and `$K$` groups.

- The coefficient of determination `$\widehat{R}{}^2$` is an upward biased estimator (too large on average).
- for the replication, `$\widehat{R}{}^2 = (4.05\times 2)/(4.05\times 2 + 82) = 0.09$`.

???

People frequently write `$\eta^2$` when they mean the estimator `$\widehat{R}{}^2$`
---

# `$\omega^2$` square estimator

Another estimator of `$\eta^2$` that is recommended in Keppel & Wickens (2004) for power calculations is `$\widehat{\omega}^2$`.

For one-way  between-subject ANOVA, the latter is obtained from the `$F$`-statistic as

`$$\widehat{\omega}^2 = \frac{\nu_1 (F-1)}{\nu_1(F-1)+n}$$`

- for the replication, `$\widehat{\omega}^2 = (2 \times 3.05)/(2 \times 3.05 + 84) = 0.0677.$`
- if the value returned is negative, report zero.

???

Since the `$F$` statistic is approximately 1 on average, this measure removes the average.

---

# Link between `$\eta^2$` to Cohen's `$f$`

Software usually take Cohen's `$f$` (or `$f^2$`) as input for the effect size.

Convert from `$\eta^2$`  (proportion of variance) to `$f$` (ratio of variance) via the relationship

`$$f^2=\frac{\eta^2}{1-\eta^2}.$$`

---

# Calculating Cohen's f

Replace `$\eta^2$` by `$\widehat{R}^2$` or `$\widehat{\omega}^2$` to get

`\begin{align*}
\widehat{f} = \sqrt{\frac{F\nu_1}{\nu_2}}, \qquad 
\widetilde{f} &= \sqrt{\frac{\nu_1(F-1)}{n}}
\end{align*}`

If we plug-in estimated values 
- with `$\widehat{R}{}^2$`, we get `$\widehat{f} = 0.314$`
- with `$\widehat{\omega}^2$`, we get `$\widetilde{f} = 0.27$`.

---

# Effect sizes for multiway ANOVA

With a completely randomized design with only experimental factors, use **partial** effect size 
`$$\eta^2_{\langle \text{effect} \rangle} = \sigma^2_{\text{effect}} / (\sigma^2_{\text{effect}} + \sigma^2_{\text{resid}})$$`

In **R**, use `effectsize::omega_squared(model, partial = TRUE)`.

]

---
# Partial effects and variance decomposition

Consider a completely randomized balanced design with two factors `$A$`, `$B$` and their interaction `$AB$`. In a balanced design, we can decompose the total variance as

`$$\sigma^2_{\text{total}} = \sigma^2_A + \sigma^2_B + \sigma^2_{AB} + \sigma^2_{\text{resid}}.$$`

Cohen's partial `$f$` measures the proportion of variability that is explained by a main effect or an interaction, e.g.,

`$$f_{\langle A \rangle}= \frac{\sigma^2_A}{\sigma^2_{\text{resid}}}, \qquad f_{\langle AB \rangle} = \frac{\sigma^2_{AB}}{\sigma^2_{\text{resid}}}.$$`

???

These variance quantities are **unknown**, so need to be estimated somehow.

---

# Partial effect size (variance)

Effect size are often reported in terms of variability via the ratio
`$$\eta^2_{\langle \text{effect} \rangle} = \frac{\sigma^2_{\text{effect}}}{\sigma^2_{\text{effect}} + \sigma^2_{\text{resid}}}.$$`

- Both `$\widehat{\eta}^2_{\langle \text{effect} \rangle}$` (aka `$\widehat{R}^2_{\langle \text{effect} \rangle}$`) and `$\widehat{\omega}^2_{\langle \text{effect} \rangle}$` are **estimators** of this quantity and obtained from the `$F$` statistic and degrees of freedom of the effect.

???

`$\widehat{\omega}^2_{\langle \text{effect} \rangle}$` is presumed less biased than `$\widehat{\eta}^2_{\langle \text{effect} \rangle}$`, as is `$\widehat{\epsilon}_{\langle \text{effect} \rangle}$`.

---

# Estimation of partial `$\omega^2$`

Similar formulas as the one-way case for between-subject experiments, with

`$$\widehat{\omega}^2_{\langle \text{effect} \rangle} = \frac{\text{df}_{\text{effect}}(F_{\text{effect}}-1)}{\text{df}_{\text{effect}}(F_{\text{effect}}-1) + n},$$`
where `$n$` is the overall sample size.

In **R**, `effectsize::omega_squared` reports these estimates with one-sided confidence intervals.

???

The confidence intervals are based on the F distribution, by changing the non-centrality parameter and inverting the distribution function (pivot method). There is a one-to-one correspondence with Cohen's f, and a bijection between the latter and omega_sq_partial or eta_sq_partial. This yields asymmetric intervals.
---

# Converting `$\omega^2$` to Cohen's `$f$`

Given an estimate of  `$\eta^2_{\langle \text{effect} \rangle}$`, convert it into an estimate of Cohen's partial `$f^2_{\langle \text{effect} \rangle}$`, e.g.,
`$$\widehat{f}^2_{\langle \text{effect} \rangle} = \frac{\widehat{\omega}^2_{\langle \text{effect}}\rangle }{1-\widehat{\omega}^2_{\langle \text{effect}}\rangle }.$$`

The package `effectsize::cohens_f` returns `$\widetilde{f}^2 = n^{-1}F_{\text{effect}}\text{df}_{\text{effect}}$`, a transformation of `$\widehat{\eta}^2_{\langle \text{effect}\rangle}$`.

---

# Summary

- Effect sizes can be recovered using information found in the ANOVA table.
- Multiple estimators for the same quantity
   - report the one used along with confidence or tolerance intervals.
   - some estimators are preferred (less biased): this matters for power studies
- The correct measure may depend on the design
   - partial vs total effects,
   - different formulas for within-subjects (repeated measures) designs!

---

layout: false
name: power
class: center middle section-title section-title-3 animated fadeIn

# Power

---

# Power and sample size calculations

Journals and grant agencies oftentimes require an estimate of the sample size needed for a study.

- large enough to pick-up effects of scientific interest (good signal-to-noise)
- efficient allocation of resources (don't waste time/money)

Same for replication studies: how many participants needed?

---

# I cried power!

.medium[
- **Power** is the ability to detect when the null is false, for a given alternative
- It is the *probability* of correctly rejecting the null hypothesis under an alternative.
- The larger the power, the better.
]

---

# Living in an alternative world

How does the _F_-test behaves under an alternative?

---

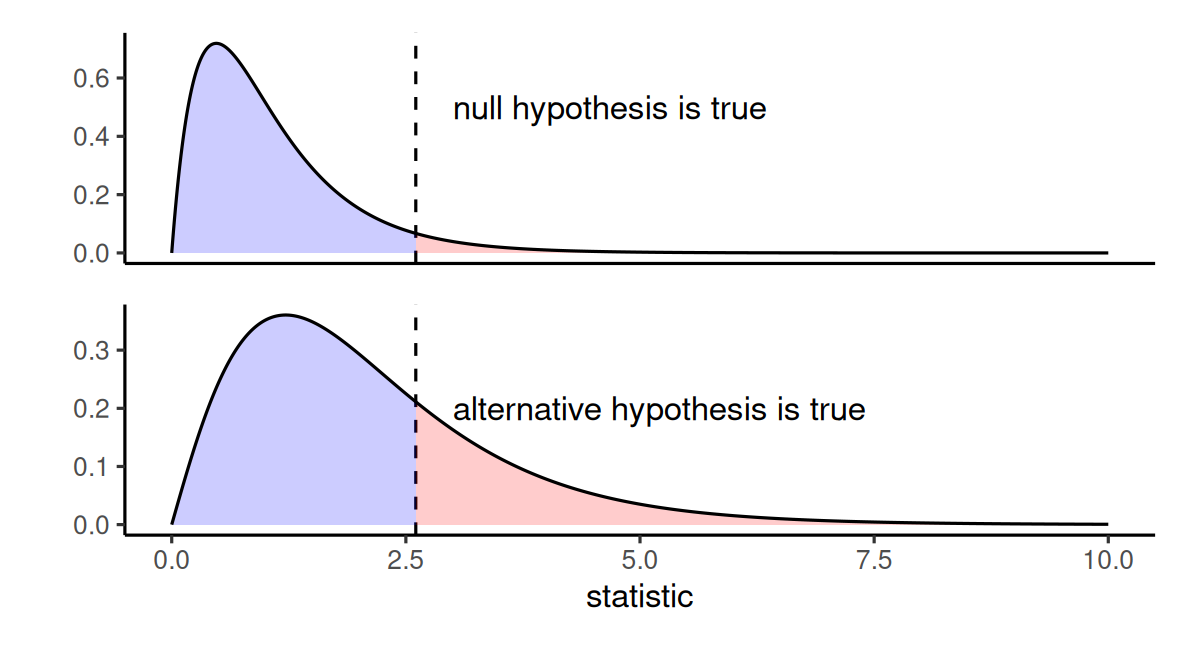
# Thinking about power

What do you think is the effect on **power** of an increase of the
- group sample size `$n_1, \ldots, n_K$`.
- variability `$\sigma^2$`.
- true mean difference `$\mu_j - \mu$`.

---

# What happens under the alternative?

The peak of the distribution shifts to the right.

Why? on average, the numerator of the `$F$`-statistic is

`$$\begin{align*}
\mathsf{E}(\text{between-group variability}) = \sigma^2+ \frac{\sum_{j=1}^K n_j(\mu_j - \mu)^2}{K-1}.
\end{align*}$$`

Under the null hypothesis, `$\mu_j=\mu$` for `$j=1, \ldots, K$`
   - the rightmost term is 0.

---

# Noncentrality parameter and power

The alternative distribution is `$F(\nu_1, \nu_2, \Delta)$` distribution with degrees of freedom `$\nu_1$` and `$\nu_2$` and noncentrality parameter 
`$$\begin{align*}
\Delta = \dfrac{\sum_{j=1}^K n_j(\mu_j - \mu)^2}{\sigma^2}.
\end{align*}$$`

---

# I cried power!

The null alternative corresponds to a single value (equality in mean), whereas there are infinitely many alternatives...

.pull-left[
<img src="09-slides_files/figure-html/powercurve1-1.png" width="80%" style="display: block; margin: auto;" />
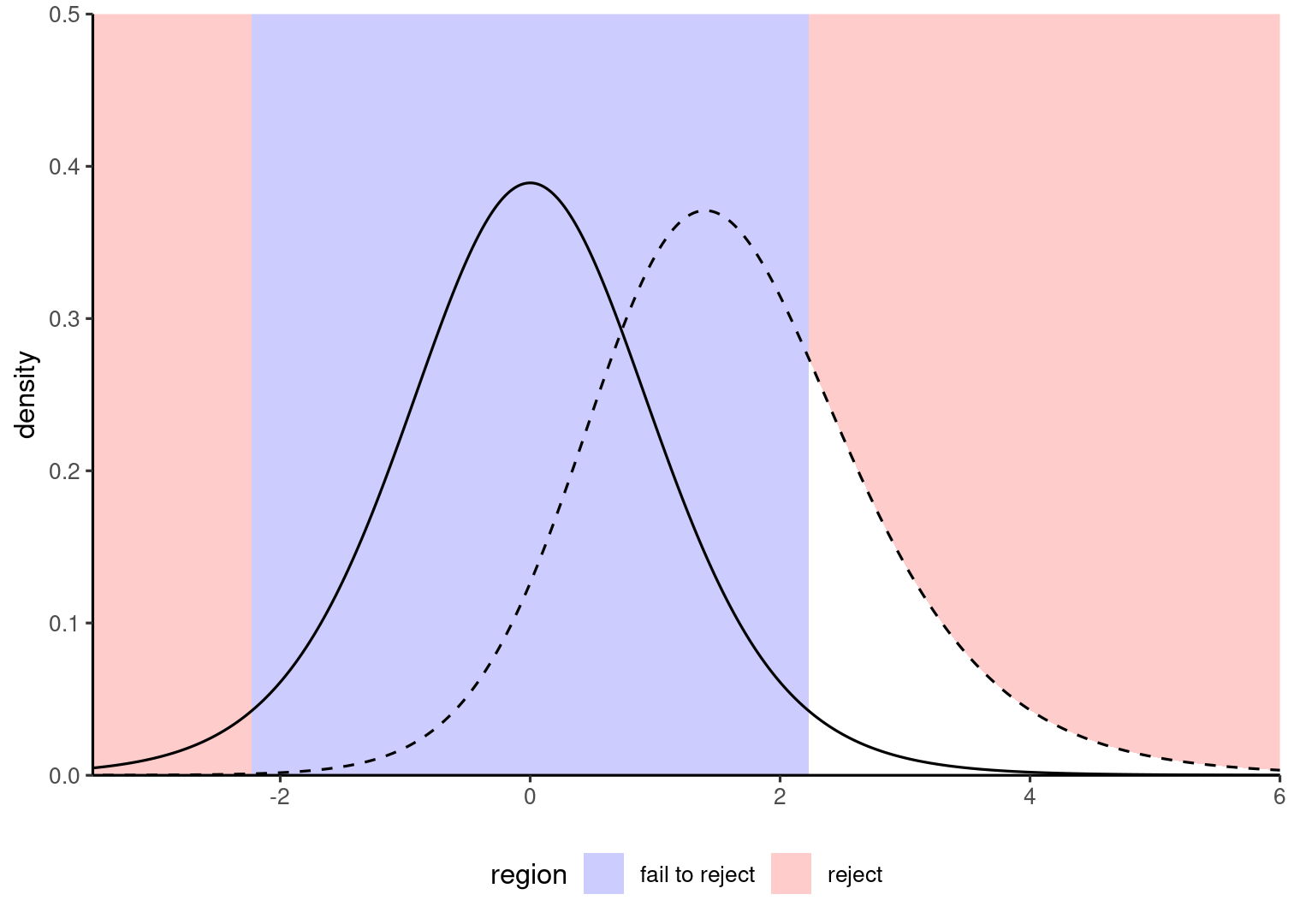  .small.center[Power is the ability to detect when the null is false, for a given alternative (dashed).]
]
.pull-right[
<img src="09-slides_files/figure-html/powercurve2-1.png" width="80%" style="display: block; margin: auto;" />
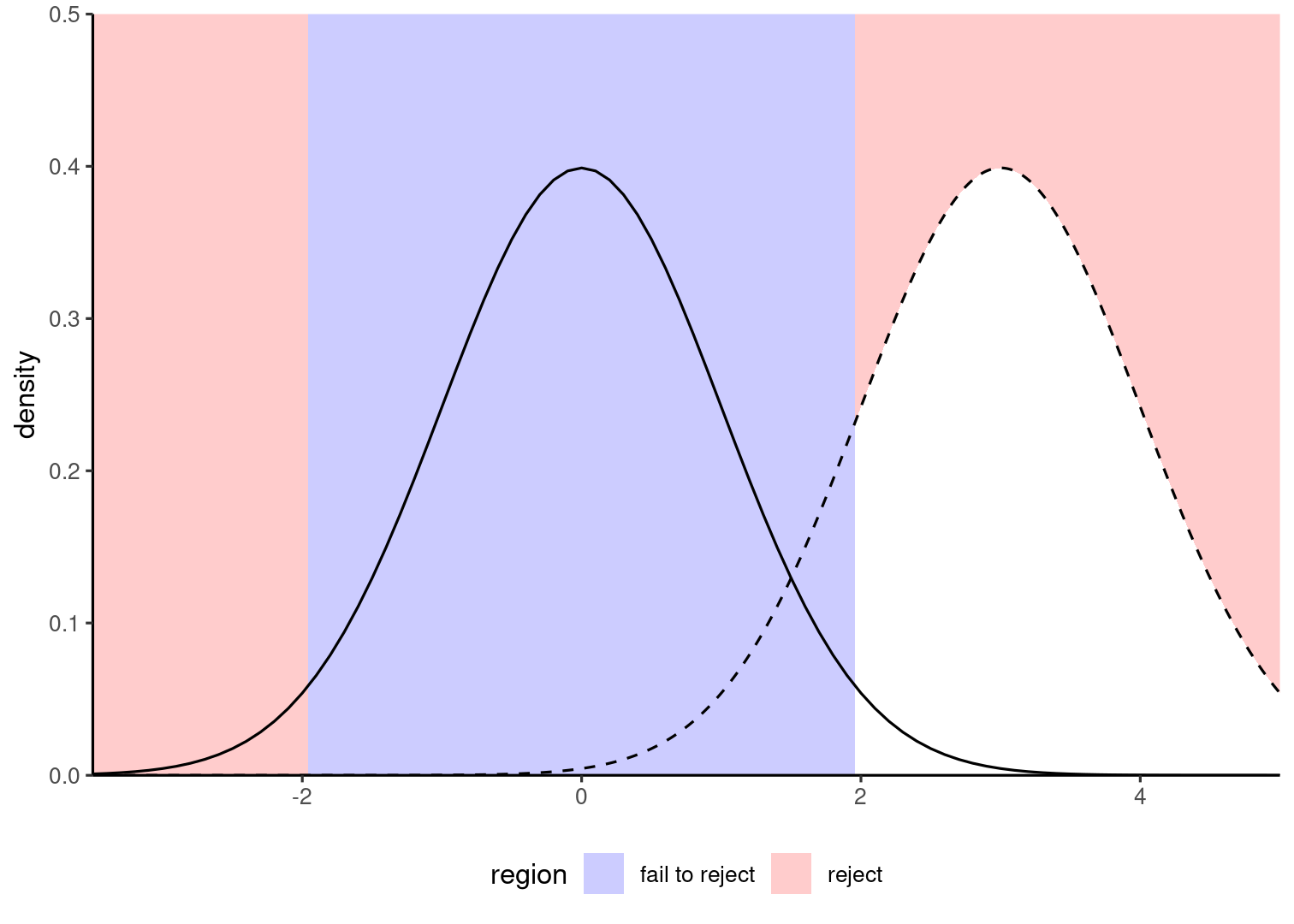 .small.center[ Power is the area in white under the dashed curved, beyond the cutoff. ]
]

???
  
In which of the two figures is power the largest?

---

# What determines power?

Think in your head of potential factors impact power for a factorial design.

1. The size of the effects, `$\delta_1 = \mu_1-\mu$`, `$\ldots$`, `$\delta_K = \mu_K-\mu$`
2. The background noise (intrinsic variability, `$\sigma^2$`)
3. The level of the test, `$\alpha$`
4. The sample size in each group, `$n_j$`
5. The choice of experimental design
6. The choice of test statistic

We focus on the interplay between

.box-3.wide[

`$\quad$` effect size `$\quad$`  |  `$\quad$`  power `$\quad$`   |  `$\quad$`  sample size `$\quad$`

]

???

The level is fixed, but we may consider multiplicity correction within the power function.
The noise level is oftentimes intrinsic to the measurement.

---

# Living in an alternative world

In a one-way ANOVA, the alternative distribution of the `$F$` test has an additional parameter `$\Delta$`, which depends on both the sample and the effect sizes.

$$
\Delta = \dfrac{\sum_{j=1}^K n_j(\mu_j - \mu)^2}{\sigma^2} = nf^2.
$$

Under the null hypothesis, `$\mu_j=\mu$` for `$j=1, \ldots, K$` and `$\Delta=0$`.

The greater `$\Delta$`, the further the mode (peak of the distribution) is from unity.

---

# Noncentrality parameter and power

$$
\Delta = \dfrac{\sum_{j=1}^K n_j(\mu_j - \mu)^2}{\sigma^2}.
$$

.box-inv-3.medium[When does power increase?]

What is the effect of an increase of the
- group sample size `$n_1, \ldots, n_K$`.
- variability `$\sigma^2$`.
- true mean difference `$\mu_j - \mu$`.

---

# Noncentrality parameter

The alternative distribution is `$F(\nu_1, \nu_2, \Delta)$` distribution with degrees of freedom `$\nu_1$` and `$\nu_2$` and noncentrality parameter `$\Delta$`.

???

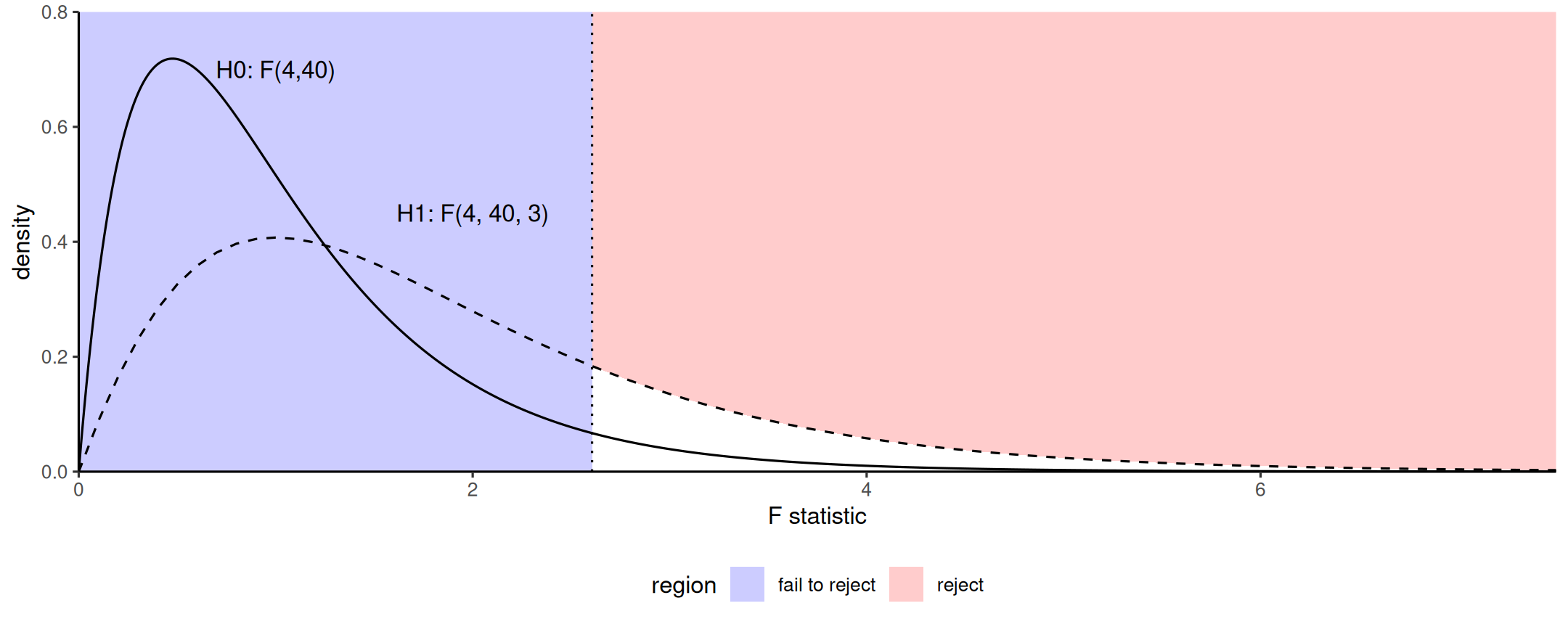
For other tests, parameters vary but the story is the same.

The plot shows the null and alternative distributions. The noncentral F is shifted to the right (mode = peak) and right skewed. The power is shaded in blue, the null distribution is shown in dashed lines.

---

# Power for factorial experiments

- `$\mathrm{G}^{\star}\mathrm{Power}$` and **R** packages take Cohen's `$f$` (or `$f^2$`) as inputs.
- Calculation based on `$F$` distribution with 
   - `$\nu_1=\text{df}_{\text{effect}}$` degrees of freedom
   - `$\nu_2 = n - n_g$`, where `$n_g$` is the number of mean parameters estimated. 
   - noncentrality parameter `$\phi = nf^2_{\langle \text{effect}\rangle}$`

---

# Example

Consider a completely randomized design with two crossed factors `$A$` and `$B$`.

We are interested by the interaction, `$\eta^2_{\langle AB \rangle}$`, and we want 80% power:

``` r
# Estimate Cohen's f from omega.sq.partial
fhat <- sqrt(omega.sq.part/(1-omega.sq.part))
# na and nb are number of levels of factors
WebPower::wp.kanova(power = 0.8, 
                    f = fhat, 
                    ndf = (na-1)*(nb-1), 
                    ng = na*nb)
```

---

# Power curves
.pull-left[

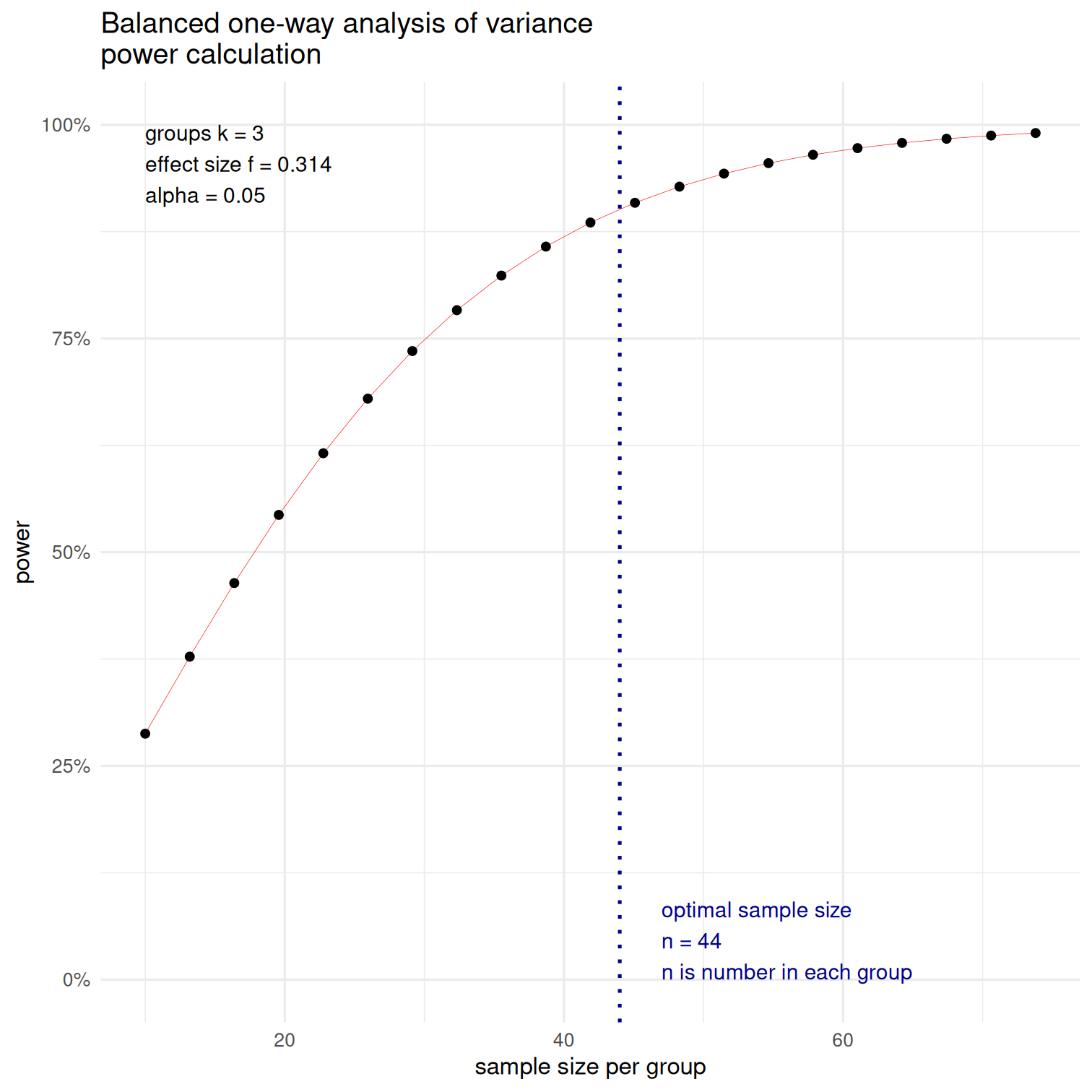
``` r
library(pwr)
power_curve <- 
 pwr.anova.test(
  f = 0.314, #from R-squared
  k = 3, 
  power = 0.9,
  sig.level = 0.05)
plot(power_curve)
```

Recall: convert `$\eta^2$` to Cohen's `$f$` (the effect size reported in `pwr`) via `$f^2=\eta^2/(1-\eta^2)$`

Using `$\widetilde{f}$` instead (from `$\widehat{\omega}^2$`) yields `$n=59$` observations per group!

]

]
.pull-right[
<img src="09-slides_files/figure-html/powercurvefig-1.png" width="504" style="display: block; margin: auto;" />
]
---

# Effect size estimates

.box-inv-3.large[WARNING!]

Most effects reported in the literature are severely inflated.

- Estimates reported in meta-analysis, etc. are not reliable. 
- Run pilot study, provide educated guesses.
- Estimated effects size are uncertain (report confidence intervals).

???

Recall the file drawer problem: most studies with small effects lead to *non significant results* and are not published. So the reported effects are larger than expected.

---

# Beware of small samples

Better to do a large replication than multiple small studies.

Otherwise, you risk being in this situation:

---

# Observed (post-hoc) power

Sometimes, the estimated values of the effect size, etc. are used as plug-in.

- The (estimated) effect size in studies are noisy! 
- Post-hoc power estimates are also noisy and typically overoptimistic.
- Not recommended, but useful pointer if the observed difference seems important (large), but there isn't enough evidence (too low signal-to-noise).

Because we reject a null doesn't mean the alternative is true!

Power is a long-term frequency property: in a given experiment, we either reject or we don't.

???

Not recommended unless the observed differences among
the means seem important in practice but
are not statistically significant