Effect size and power

# Effect size and power

**Session 9**

]

---

# Outline
--

.box-1.large.sp-after-half[Effect sizes]

.box-3.large.sp-after-half[Power]

---
layout: false
name: effect
class: center middle section-title section-title-1 animated fadeIn

# Effect size

---
layout: true
class: title title-1

---

# Motivating example

Quote from the OSC psychology replication

> The key statistics provided in the paper to test the “depletion” hypothesis is the main effect of a one-way ANOVA with three experimental conditions and confirmatory information processing as the dependent variable; `$F(2, 82) = 4.05$`, `$p = 0.02$`, `$\eta^2 = 0.09$`. Considering the original effect size and an alpha of `$0.05$` the sample size needed to achieve `$90$`% power is `$132$` subjects.

.small[
Replication report of Fischer, Greitemeyer, and Frey (2008, JPSP, Study 2) by E.M. Galliani
]

---

# Translating statement into science

.box-inv-1.medium.sp-after-half[Q: How many observations should <br>I gather to reliably detect an effect?]
.box-inv-1.medium.sp-after-half[Q: How big is this effect?]

---

# Does it matter?

With large enough sample size, **any** sized difference between treatments becomes statistically significant.

.box-inv-1.medium.sp-before-half[
Statistical significance `$\neq$` practical relevance
]

But whether this is important depends on the scientific question.

---

# Example

- What is the minimum difference between two treatments that would be large enough to justify commercialization of a drug?
- Tradeoff between efficacy of new treatment vs status quo, cost of drug, etc.

---

# Using statistics to measure effects

Statistics and `$p$`-values are not good summaries of magnitude of an effect:

- the larger the sample size, the bigger the statistic, the smaller the `$p$`-value

Instead use

.pull-left[
.box-inv-1[standardized differences]
]
.pull-right[
.box-inv-1[percentage of variability explained]
]

Estimators popularized in the handbook
> Cohen, Jacob. Statistical Power Analysis for the Behavioral Sciences, 2nd ed., Routhledge, 1988.

---

# Illustrating effect size (differences)

.tiny[
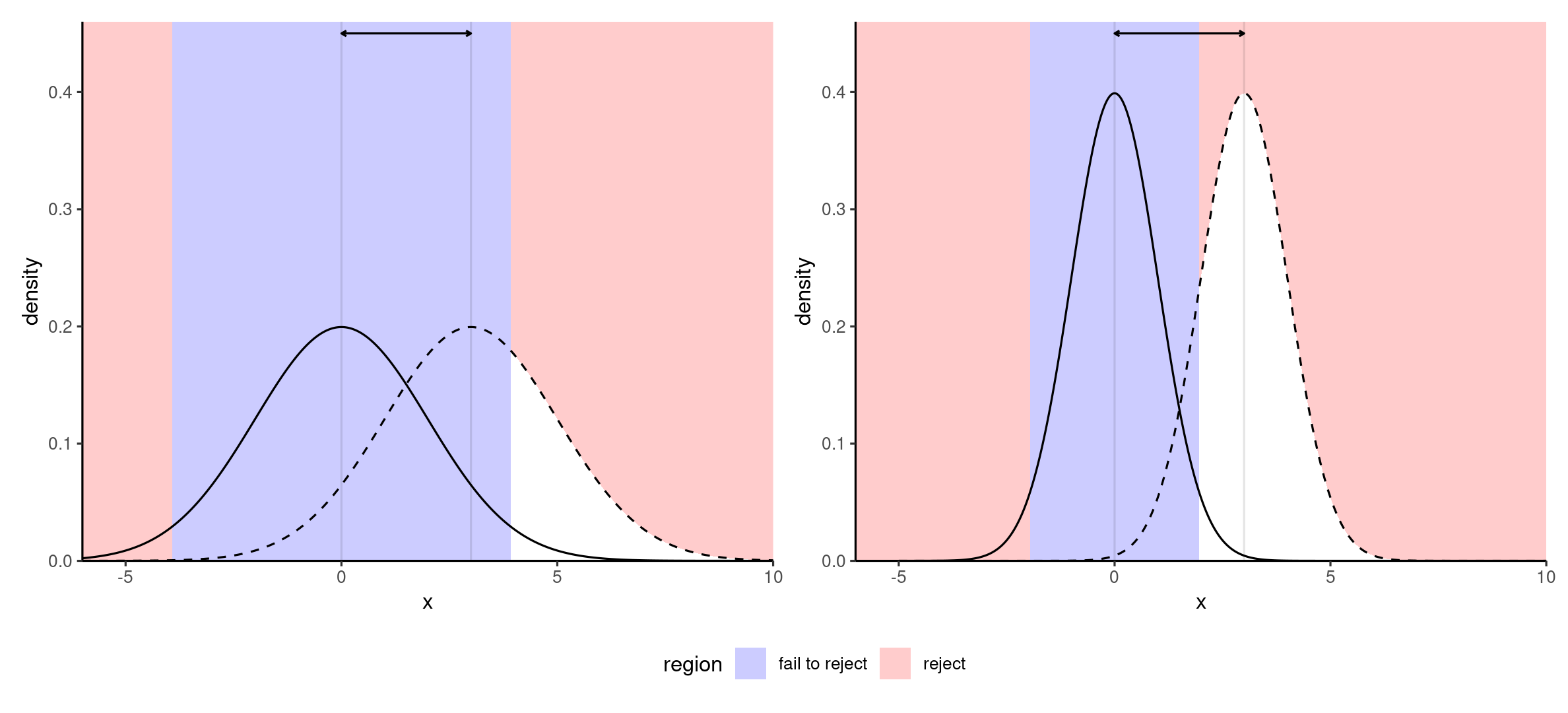
The plot shows null (thick) and true sampling distributions (dashed) for the same difference in sample mean with small (left) and large (right) samples.
]
---

# Estimands, estimators, estimates

- `$\mu_i$` is the (unknown) population mean of group `$i$` (parameter, or estimand)
- `$\widehat{\mu}_i$` is a formula (an estimator) that takes data as input and returns a numerical value (an estimate).
- throughout, use hats to denote estimated quantities:

.pull-left-3[
<img src="img/08/estimand.jpg" width="90%" style="display: block; margin: auto;" />
]
.pull-middle-3[
<img src="img/08/estimator.jpg" width="90%" style="display: block; margin: auto;" />
]

.tiny[
Left to right: parameter `$\mu$` (target), estimator `$\widehat{\mu}$` (recipe) and estimate `$\widehat{\mu}=10$` (numerical value, proxy)
]

???

From Twitter, @simongrund89

---

# Cohen's _d_

Standardized measure of effect (dimensionless=no units):

Assuming equal variance `$\sigma^2$`, compare mean of two groups `$i$` and `$j$`:

$$
d = \frac{\mu_i - \mu_j}{\sigma}
$$

- Usual estimator of Cohen's `$d$`, `$\widehat{d}$`, uses sample average of groups and the pooled variance estimator `$\widehat{\sigma}$`.

Cohen's classification: small (_d=0.2_), medium (_d=0.5_) or large (_d=0.8_) effect size.

???

Note: this is not the `$t$`-statistic (the denominator is the estimated standard deviation, not the standard error of the mean

Note that there are multiple versions of Cohen's coefficients. 
These are the effects of the pwr package.
The small/medium/large effect size varies depending on the test! See the vignette of pwr for defaults.

---

# Cohen's _f_

For a one-way ANOVA (equal variance `$\sigma^2$`) with more than two groups,

$$
f^2 = \frac{1}{\sigma^2} \sum_{j=1}^k \frac{n_j}{n}(\mu_j - \mu)^2,
$$
a weighted sum of squared difference relative to the overall mean `$\mu$`.

For `$k=2$` groups, Cohen's `$f$` and Cohen's `$d$` are related via `$f=d/2$`.

---

# Effect size: proportion of variance

If there is a single experimental factor, use **total** effect size.

Break down the variability `$$\sigma^2_{\text{total}} = \sigma^2_{\text{resid}} + \sigma^2_{\text{effect}}$$` and define the percentage of variability explained by the `$\text{effect}$`.
`$$\eta^2 = \frac{\text{explained variability}}{\text{total variability}}= \frac{\sigma^2_{\text{effect}}}{\sigma^2_{\text{total}}}.$$`
 
---

# Coefficient of determination estimator

For the balanced one-way between-subject ANOVA, typical estimator is the **coefficient of determination**

$$
\widehat{R}{}^2 = \frac{F\nu_1}{F\nu_1 + \nu_2}
$$
where `$\nu_1 = K-1$` and `$\nu_2 = n-K$` are the degrees of freedom for the one-way ANOVA with `$n$` observations and `$K$` groups.

- `$\widehat{R}{}^2$` is an upward biased estimator (too large on average).
- People frequently write `$\eta^2$` when they mean `$\widehat{R}{}^2$`
- for the replication, `$\widehat{R}{}^2 = (4.05\times 2)/(4.05\times 2 + 82) = 0.09$`

---

# `$\omega^2$` square estimator

Another estimator of `$\eta^2$` that is recommended in Keppel & Wickens (2004) for power calculations is `$\widehat{\omega}^2$`.

For one-way  between-subject ANOVA, the latter is obtained from the `$F$`-statistic as

`$$\widehat{\omega}^2 = \frac{\nu_1 (F-1)}{\nu_1(F-1)+n}$$`

- for the replication, `$\widehat{\omega}^2 = (3.05\times 2)/(3.05\times 2 + 84) = 0.0677.$`
- if the value returned is negative, report zero.

???

Since the `$F$` statistic is approximately 1 on average, this measure removes the average.

---

# Converting `$\eta^2$` to Cohen's `$f$`

Software usually take Cohen's `$f$` (or `$f^2$`) as input for the effect size.

Convert from `$\eta$` to `$f$` via the relationship

`$$f^2=\frac{\eta^2}{1-\eta^2}.$$`

If we plug-in estimated values 
- with `$\widehat{R}{}^2$`, we get `$\widehat{f} = 0.314$`
- with `$\widehat{\omega}^2$`, we get `$\widetilde{f} = 0.27$`.

---

# Effect sizes for multiway ANOVA

With a completely randomized design with only experimental factors, use **partial** effect size 
`$$\eta^2_{\langle \text{effect} \rangle} = \sigma^2_{\text{effect}} / (\sigma^2_{\text{effect}} + \sigma^2_{\text{resid}})$$`

In **R**, use `effectsize::omega_squared(model, partial = TRUE)`.

]

---
# Partial effects and variance decomposition

Consider a completely randomized balanced design with two factors `$A$`, `$B$` and their interaction `$AB$`. In a balanced design, we can decompose the total variance as

`$$\sigma^2_{\text{total}} = \sigma^2_A + \sigma^2_B + \sigma^2_{AB} + \sigma^2_{\text{resid}}.$$`

Cohen's partial `$f$` measures the proportion of variability that is explained by a main effect or an interaction, e.g.,

`$$f_{\langle A \rangle}= \frac{\sigma^2_A}{\sigma^2_{\text{resid}}}, \qquad f_{\langle AB \rangle} = \frac{\sigma^2_{AB}}{\sigma^2_{\text{resid}}}.$$`

???

These variance quantities are **unknown**, so need to be estimated somehow.

---

# Partial effect size (variance)

Effect size are often reported in terms of variability via the ratio
`$$\eta^2_{\langle \text{effect} \rangle} = \frac{\sigma^2_{\text{effect}}}{\sigma^2_{\text{effect}} + \sigma^2_{\text{resid}}}.$$`

- Both `$\widehat{\eta}^2_{\langle \text{effect} \rangle}$` (aka `$\widehat{R}^2_{\langle \text{effect} \rangle}$`) and `$\widehat{\omega}^2_{\langle \text{effect} \rangle}$` are **estimators** of this quantity and obtained from the `$F$` statistic and degrees of freedom of the effect.

???

`$\widehat{\omega}^2_{\langle \text{effect} \rangle}$` is presumed less biased than `$\widehat{\eta}^2_{\langle \text{effect} \rangle}$`, as is `$\widehat{\epsilon}_{\langle \text{effect} \rangle}$`.

---

# Estimation of partial `$\omega^2$`

Similar formulas as the one-way case for between-subject experiments, with

`$$\widehat{\omega}^2_{\langle \text{effect} \rangle} = \frac{\text{df}_{\text{effect}}(F_{\text{effect}}-1)}{\text{df}_{\text{effect}}(F_{\text{effect}}-1) + n},$$`
where `$n$` is the overall sample size.

In **R**, `effectsize::omega_squared` reports these estimates with one-sided confidence intervals.

???

The confidence intervals are based on the F distribution, by changing the non-centrality parameter and inverting the distribution function (pivot method). There is a one-to-one correspondence with Cohen's f, and a bijection between the latter and omega_sq_partial or eta_sq_partial. This yields asymmetric intervals.
---

# Converting `$\omega^2$` to Cohen's `$f$`

Given an estimate of  `$\eta^2_{\langle \text{effect} \rangle}$`, convert it into an estimate of Cohen's partial `$f^2_{\langle \text{effect} \rangle}$`, e.g.,
`$$\widehat{f}^2_{\langle \text{effect} \rangle} = \frac{\widehat{\omega}^2_{\langle \text{effect}}\rangle }{1-\widehat{\omega}^2_{\langle \text{effect}}\rangle }.$$`

The package `effectsize::cohens_f` returns `$\widetilde{f}^2 = n^{-1}F_{\text{effect}}\text{df}_{\text{effect}}$`, a transformation of `$\widehat{\eta}^2_{\langle \text{effect}\rangle}$`.

---

# Summary

- Effect sizes can be recovered using information found in the ANOVA table.
- Multiple estimators for the same quantity
   - report the one used along with confidence or tolerance intervals.
   - some estimators are preferred (less biased): this matters for power studies
- The correct measure may depend on the design
   - partial vs total effects,
   - different formulas for within-subjects (repeated measures) designs!

---

layout: false
name: power
class: center middle section-title section-title-3 animated fadeIn

# Power

---

# Power and sample size calculations

Journals and grant agencies oftentimes require an estimate of the sample size needed for a study.

- large enough to pick-up effects of scientific interest (good signal-to-noise)
- efficient allocation of resources (don't waste time/money)

Same for replication studies: how many participants needed?

---

# I cried power!

.medium[
- **Power** is the ability to detect when the null is false, for a given alternative
- It is the *probability* of correctly rejecting the null hypothesis under an alternative.
- The larger the power, the better.
]

---

# Living in an alternative world

How does the _F_-test behaves under an alternative?

---

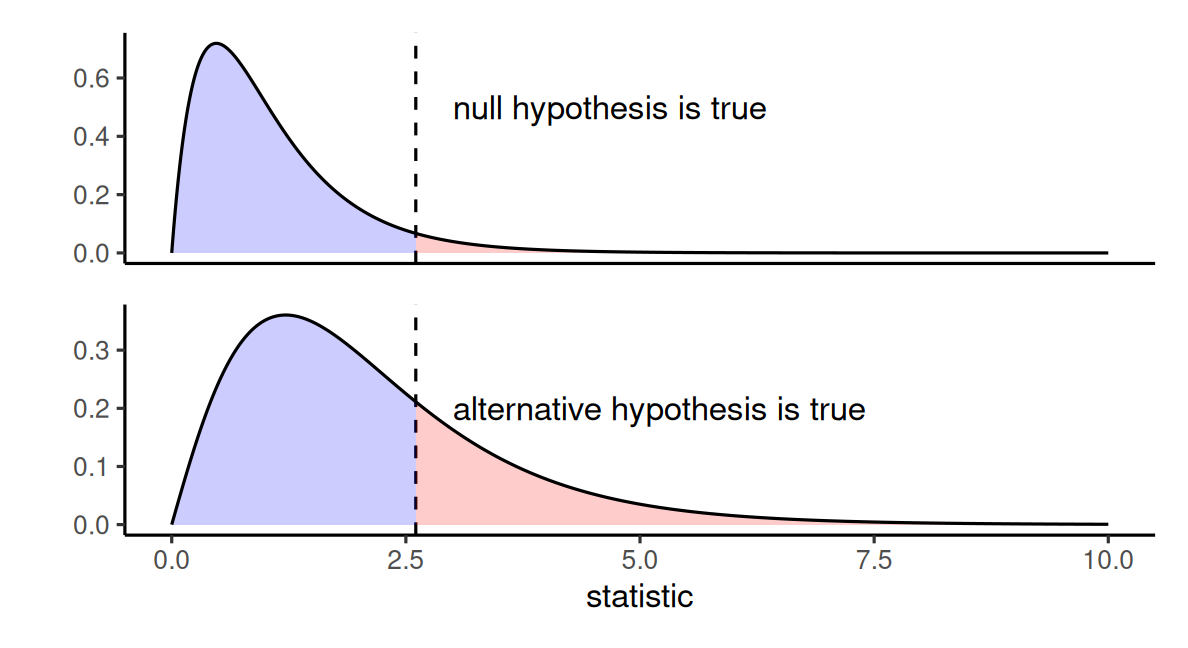
# Thinking about power

What do you think is the effect on **power** of an increase of the
- group sample size `$n_1, \ldots, n_K$`.
- variability `$\sigma^2$`.
- true mean difference `$\mu_j - \mu$`.

---

# What happens under the alternative?

The peak of the distribution shifts to the right.

Why? on average, the numerator of the `$F$`-statistic is

`$$\begin{align*}
\mathsf{E}(\text{between-group variability}) = \sigma^2+ \frac{\sum_{j=1}^K n_j(\mu_j - \mu)^2}{K-1}.
\end{align*}$$`

Under the null hypothesis, `$\mu_j=\mu$` for `$j=1, \ldots, K$`
   - the rightmost term is 0.

---

# Noncentrality parameter and power

The alternative distribution is `$F(\nu_1, \nu_2, \Delta)$` distribution with degrees of freedom `$\nu_1$` and `$\nu_2$` and noncentrality parameter 
`$$\begin{align*}
\Delta = \dfrac{\sum_{j=1}^K n_j(\mu_j - \mu)^2}{\sigma^2}.
\end{align*}$$`

---

# I cried power!

The null alternative corresponds to a single value (equality in mean), whereas there are infinitely many alternatives...

.pull-left[
<img src="09-slides_files/figure-html/powercurve1-1.png" width="80%" style="display: block; margin: auto;" />
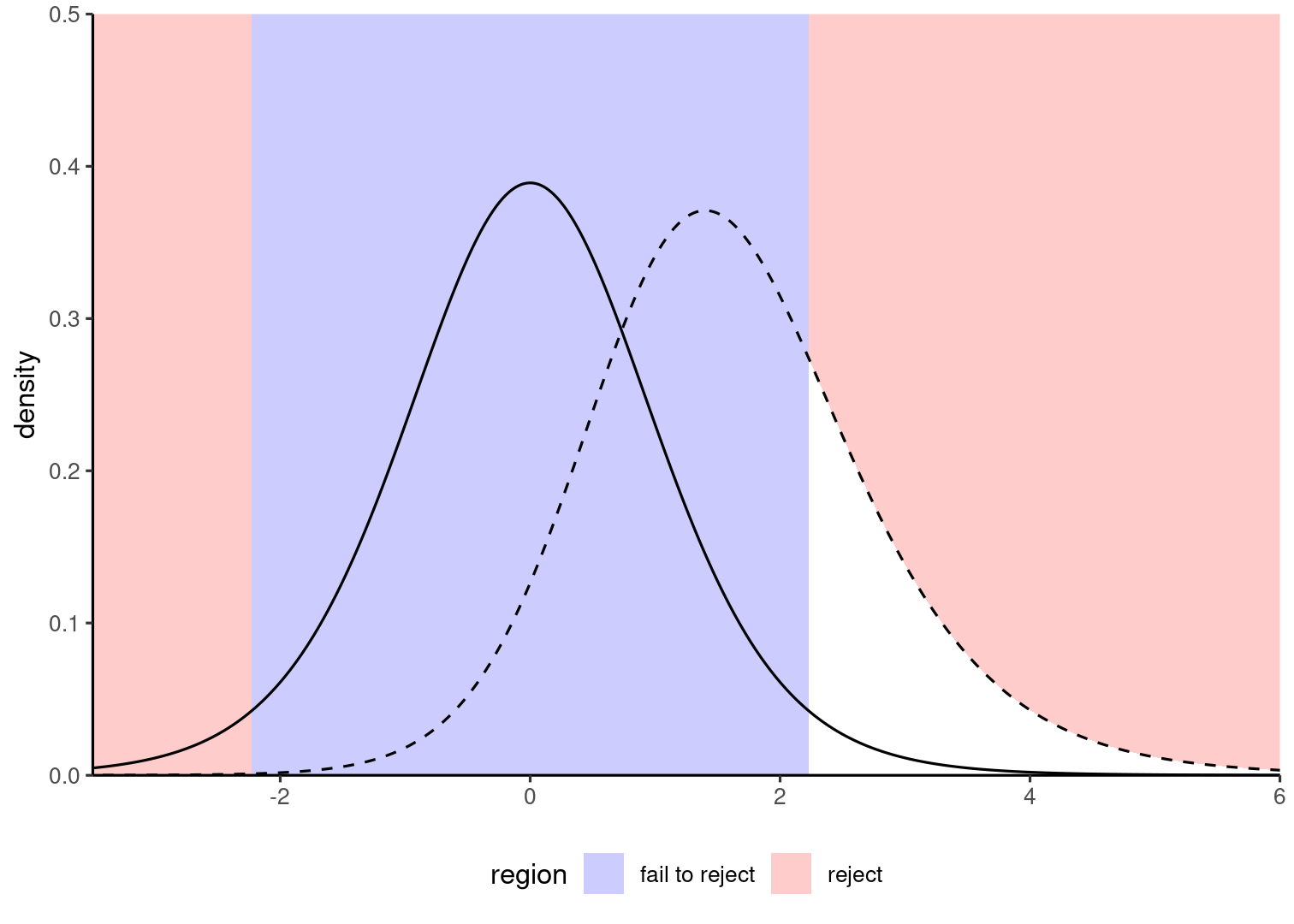  .small.center[Power is the ability to detect when the null is false, for a given alternative (dashed).]
]
.pull-right[
<img src="09-slides_files/figure-html/powercurve2-1.png" width="80%" style="display: block; margin: auto;" />
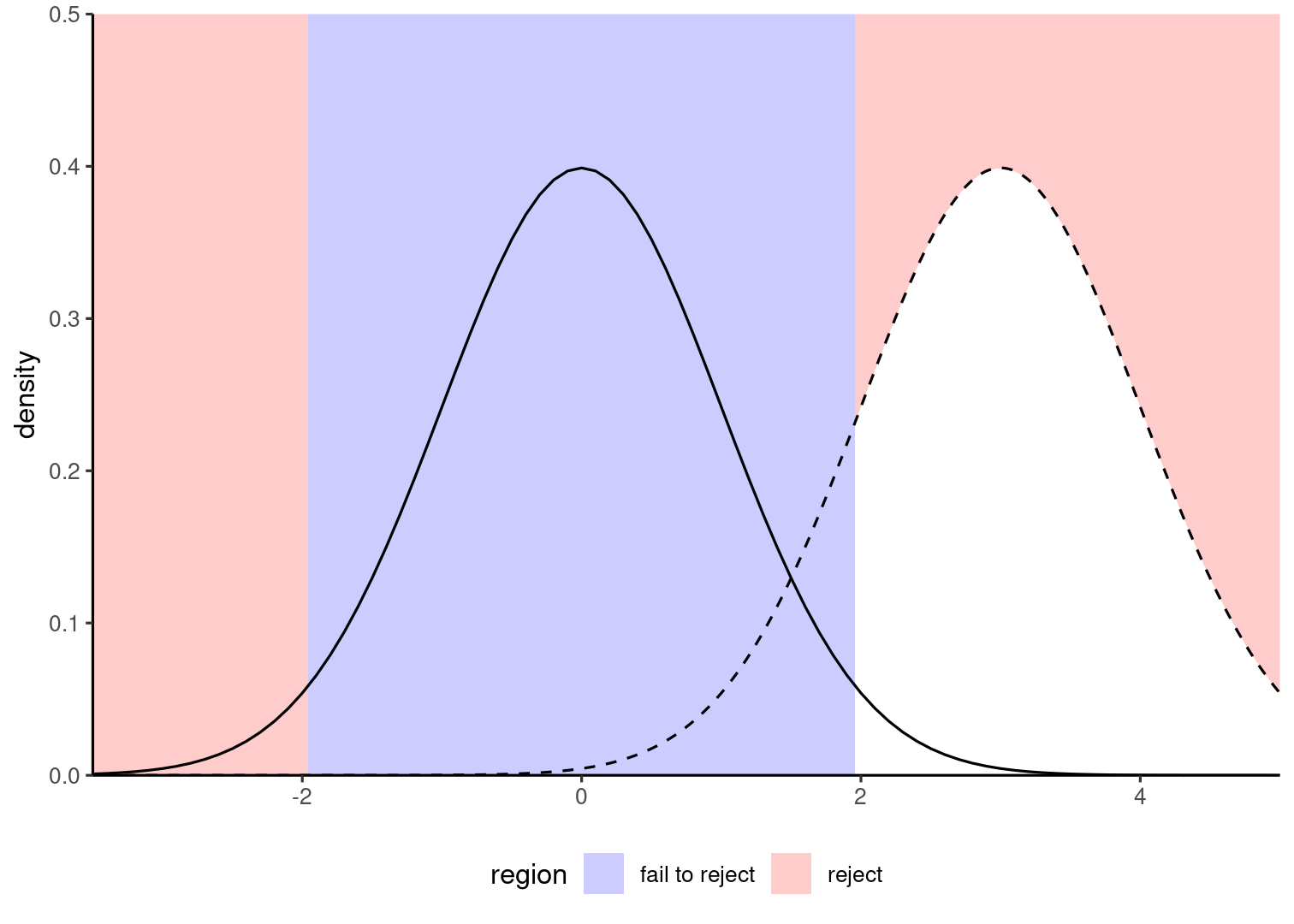 .small.center[ Power is the area in white under the dashed curved, beyond the cutoff. ]
]

???
  
In which of the two figures is power the largest?

---

# What determines power?

Think in your head of potential factors impact power for a factorial design.

1. The size of the effects, `$\delta_1 = \mu_1-\mu$`, `$\ldots$`, `$\delta_K = \mu_K-\mu$`
2. The background noise (intrinsic variability, `$\sigma^2$`)
3. The level of the test, `$\alpha$`
4. The sample size in each group, `$n_j$`
5. The choice of experimental design
6. The choice of test statistic

We focus on the interplay between

.box-3.wide[

`$\quad$` effect size `$\quad$`  |  `$\quad$`  power `$\quad$`   |  `$\quad$`  sample size `$\quad$`

]

???

The level is fixed, but we may consider multiplicity correction within the power function.
The noise level is oftentimes intrinsic to the measurement.

---

# Living in an alternative world

In a one-way ANOVA, the alternative distribution of the `$F$` test has an additional parameter `$\Delta$`, which depends on both the sample and the effect sizes.

$$
\Delta = \dfrac{\sum_{j=1}^K n_j(\mu_j - \mu)^2}{\sigma^2} = nf^2.
$$

Under the null hypothesis, `$\mu_j=\mu$` for `$j=1, \ldots, K$` and `$\Delta=0$`.

The greater `$\Delta$`, the further the mode (peak of the distribution) is from unity.

---

# Noncentrality parameter and power

$$
\Delta = \dfrac{\sum_{j=1}^K n_j(\mu_j - \mu)^2}{\sigma^2}.
$$

.box-inv-3.medium[When does power increase?]

What is the effect of an increase of the
- group sample size `$n_1, \ldots, n_K$`.
- variability `$\sigma^2$`.
- true mean difference `$\mu_j - \mu$`.

---

# Noncentrality parameter

The alternative distribution is `$F(\nu_1, \nu_2, \Delta)$` distribution with degrees of freedom `$\nu_1$` and `$\nu_2$` and noncentrality parameter `$\Delta$`.

???

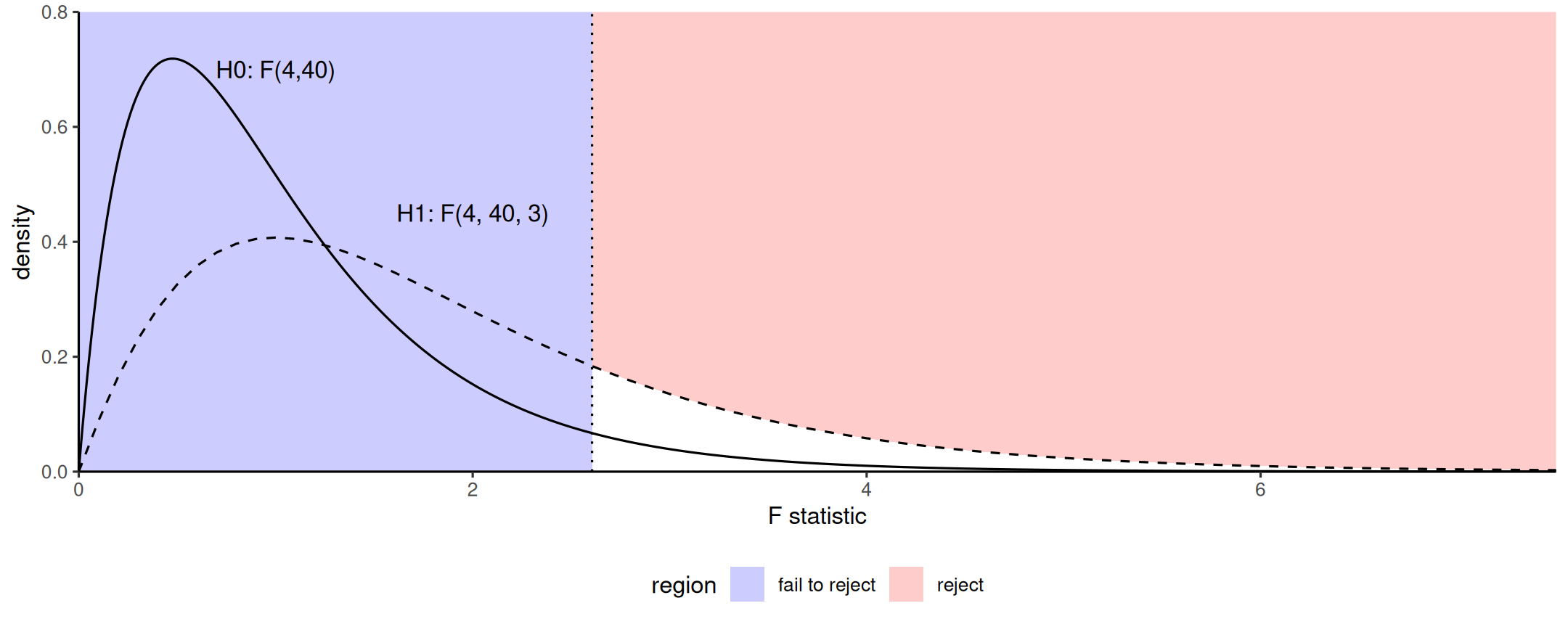
For other tests, parameters vary but the story is the same.

The plot shows the null and alternative distributions. The noncentral F is shifted to the right (mode = peak) and right skewed. The power is shaded in blue, the null distribution is shown in dashed lines.

---

# Power for factorial experiments

- `$\mathrm{G}^{\star}\mathrm{Power}$` and **R** packages take Cohen's `$f$` (or `$f^2$`) as inputs.
- Calculation based on `$F$` distribution with 
   - `$\nu_1=\text{df}_{\text{effect}}$` degrees of freedom
   - `$\nu_2 = n - n_g$`, where `$n_g$` is the number of mean parameters estimated. 
   - noncentrality parameter `$\phi = nf^2_{\langle \text{effect}\rangle}$`

---

# Example

Consider a completely randomized design with two crossed factors `$A$` and `$B$`.

We are interested by the interaction, `$\eta^2_{\langle AB \rangle}$`, and we want 80% power:

``` r
# Estimate Cohen's f from omega.sq.partial
fhat <- sqrt(omega.sq.part/(1-omega.sq.part))
# na and nb are number of levels of factors
WebPower::wp.kanova(power = 0.8, 
                    f = fhat, 
                    ndf = (na-1)*(nb-1), 
                    ng = na*nb)
```

---

# Power curves
.pull-left[

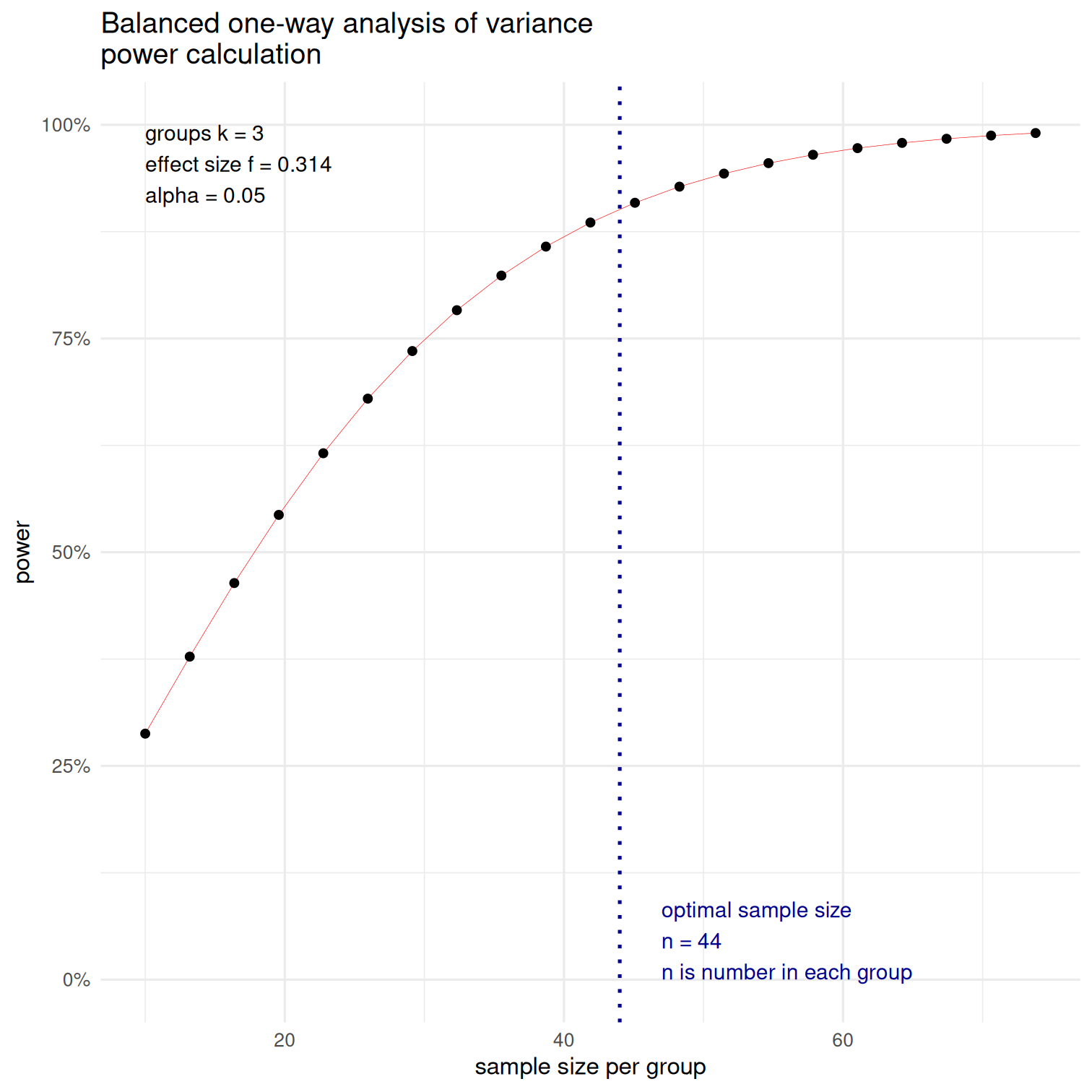
``` r
library(pwr)
power_curve <- 
 pwr.anova.test(
  f = 0.314, #from R-squared
  k = 3, 
  power = 0.9,
  sig.level = 0.05)
plot(power_curve)
```

Recall: convert `$\eta^2$` to Cohen's `$f$` (the effect size reported in `pwr`) via `$f^2=\eta^2/(1-\eta^2)$`

Using `$\widetilde{f}$` instead (from `$\widehat{\omega}^2$`) yields `$n=59$` observations per group!

]

]
.pull-right[
<img src="09-slides_files/figure-html/powercurvefig-1.png" width="504" style="display: block; margin: auto;" />
]
---

# Effect size estimates

.box-inv-3.large[WARNING!]

Most effects reported in the literature are severely inflated.

- Estimates reported in meta-analysis, etc. are not reliable. 
- Run pilot study, provide educated guesses.
- Estimated effects size are uncertain (report confidence intervals).

???

Recall the file drawer problem: most studies with small effects lead to *non significant results* and are not published. So the reported effects are larger than expected.

---

# Beware of small samples

Better to do a large replication than multiple small studies.

Otherwise, you risk being in this situation:

---

# Observed (post-hoc) power

Sometimes, the estimated values of the effect size, etc. are used as plug-in.

- The (estimated) effect size in studies are noisy! 
- Post-hoc power estimates are also noisy and typically overoptimistic.
- Not recommended, but useful pointer if the observed difference seems important (large), but there isn't enough evidence (too low signal-to-noise).

Because we reject a null doesn't mean the alternative is true!

Power is a long-term frequency property: in a given experiment, we either reject or we don't.

???

Not recommended unless the observed differences among
the means seem important in practice but
are not statistically significant