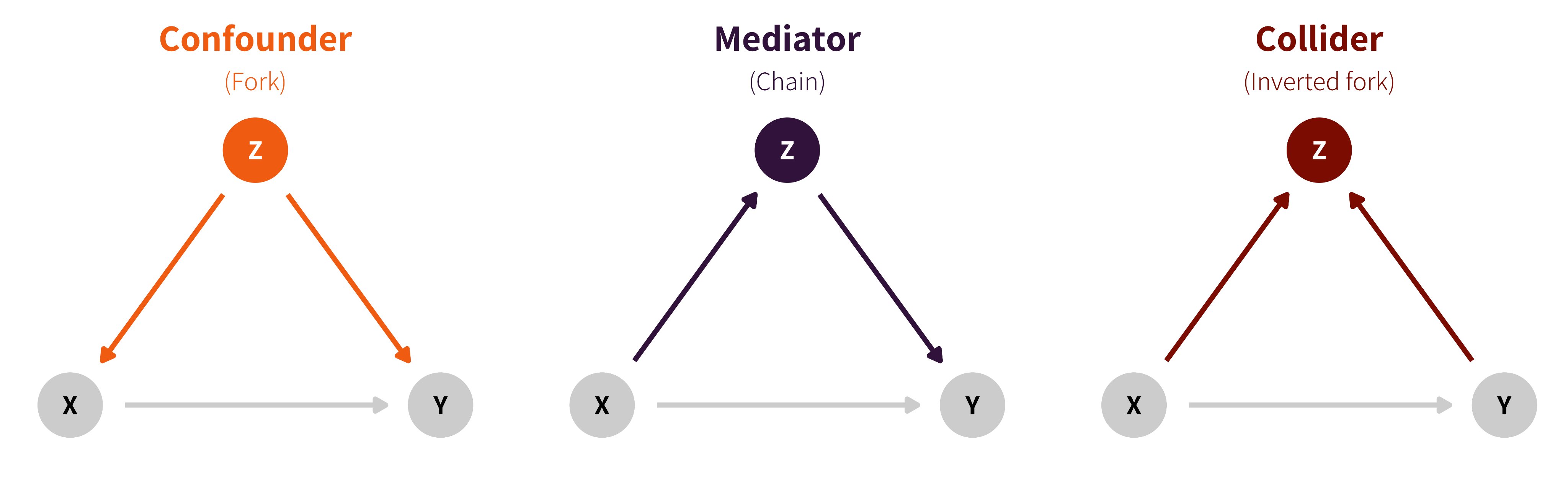
Reminder: three types of causal associations

Notation

Define

• treatment of individual $i$ as $X_i$, typically binary or categorical with $X_i\in \{0,\dots ,K\}$ and
  • $X=0$ (control)
  • $X=k$ (treatment) for $k=1,\dots ,K$
• potential mediation given treatment $x$ as $M_i\left(x\right)$ and
• potential outcome for treatment $x$ and mediator $m$ as $Y_i(x,m)$.

Sequential ignorability assumption

1. Given pre-treatment covariates $Z$, potential outcomes for mediation and treatment are conditionally independent of treatment assignment. $$Y_i(x^{\prime },m),M_i\left(x\right)\perp \perp X_i\mid Z_i=z$$
2. Given pre-treatment covariates $Z$ and observed treatment $x$, potential outcomes for the response are independent of mediation. $$Y_i(x^{\prime },m)\perp \perp M_i\left(x\right)\mid X_i=x,Z_i=z$$

• Assumption 1 holds under randomization of treatment.
• Assumption 2 implies there is no confounder affecting both $Y_i,M_i$.

Directed acyclic graph

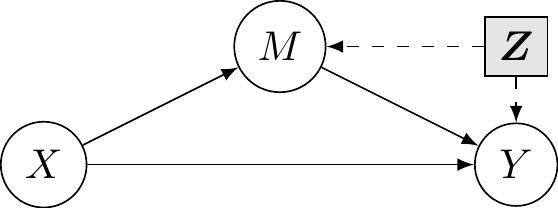
Directed acyclic graph of the linear mediation model

Average directed effect

The $ADE$ measures the flow along $X\to Y$, disabling the pathway $X\to M\to Y$ by fixing the mediator value: it is $$\begin{array}{cc}ADE\left(x\right)& =E\left[Y_i\right(1,M_i\left(x\right))-Y_i(0,M_i\left(x\right)\left)\right\}\end{array}$$

This measures the expected change in response when the experimental factor changes from treatment to control, while the mediator is set to a fixed value $M_i\left(x\right)$ uniformly over the population. Fixing the mediator may or not be feasible experimentally.

If there is no interaction between the treatment and the mediator, then $ADE\left(0\right)=ADE\left(1\right)$.

Average causal mediation effect

Also called indirect effect, obtained for a fixed intervention due to changing the values of the mediator to those it would take under the treatment and control group, respectively $M_i\left(1\right)$ and $M_i\left(0\right)$.

$$\begin{array}{cc}ACME\left(x\right)& =E\left[Y_i\right\{x,M_i\left(1\right)\}-Y_i\{x,M_i\left(0\right)\left\}\right]\end{array}$$

If there is no interaction between the treatment and the mediator, then $ACME\left(0\right)=ACME\left(1\right)$

Total effect

Total effect: overall impact of $X$ (both through $M$ and directly)

$$\begin{array}{c}TE=E[Y\mid \text{do}(X=1\left)\right]-E[Y\mid \text{do}(X=0\left)\right]\end{array}$$

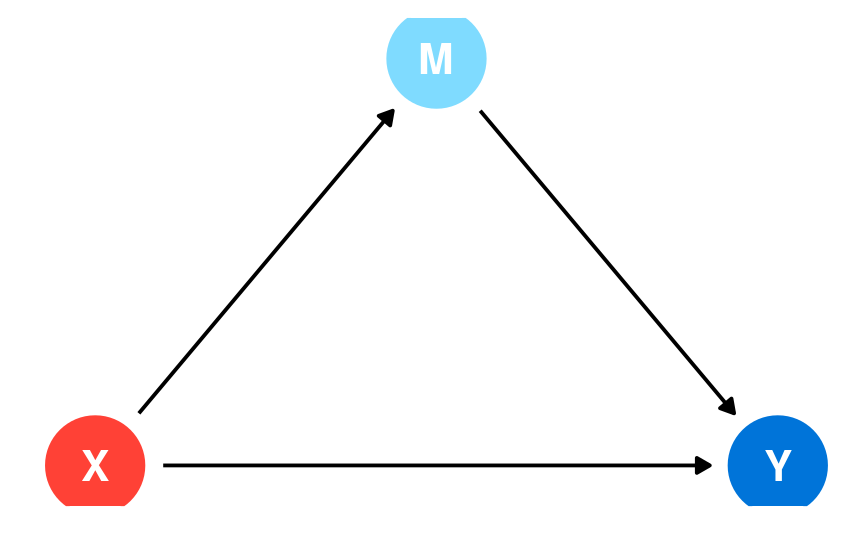
The total effect is the average change in response if we randomize treatment assignment and consider the difference treatment vs control.

Total effect

The total effect measures the average overall impact of changes in outcome $Y$ (both through $M$ and directly) when experimentally manipulating $X$, $$\begin{array}{cc}TE& =E\left[Y_i\right\{1,M\left(1\right)\left\}\right]-E\left[Y_i\right\{0,M\left(0\right)\left\}\right],\end{array}$$

• The total effect is obtained as $$TE=ACME\left(X\right)+ADE(1-X),X=0,1.$$

Linear mediation model

Consider the following two linear regression models with a binary treatment $X\in \{0,1\}$ and $M$ binary or continuous:

$$\begin{array}{cc}\underset{d\text{mediator}}{M\beta }& =\underset{d\text{intercept}}{c_m\beta }+\alpha X+\underset{\text{error term}}{{\epsilon }_m\beta }\\ \underset{d\text{response}}{Y\beta }& =\underset{\text{intercept}}{c_y\beta }+\underset{\text{direct effect}}{\beta X}+\gamma M+\underset{\text{error term}}{{\epsilon }_y\beta }\end{array}$$

We assume that zero-mean error terms ${\epsilon }_m$ and ${\epsilon }_y$ are uncorrelated.

• This is tied to the no confounders assumption.

Total effect decomposition

Plugging the first equation in the second, we get the marginal model for $Y$ given treatment $X$ $$\begin{array}{cc}E(Y\mid X=x)& =\underset{\text{intercept}}{(c_y+\gamma c_m)}+\underset{\text{total effect}}{(\beta +\alpha \gamma )}\cdot x\end{array}$$

In an experiment, we can obtain the total effect via the ANOVA model, with

$$\begin{array}{cc}Y& =\underset{\text{average of control}}{\nu }+\underset{\text{total effect}}{\tau X}+\underset{\text{error term}}{{\epsilon }_{Y^{\prime }}}\\ \tau & =E\{Y\mid do(X=1\left)\right\}-E\{Y\mid do(X=0\left)\right\}\end{array}$$

Product of coefficient method

In the linear mediation model of Baron and Kenny, the quantities of interest are

$$\begin{array}{cc}ACME\left(x\right)& =E\left[Y\right\{x,M\left(1\right)\}-Y\{x,M\left(0\right)\left\}\right]=\alpha \gamma \\ ADE\left(x\right)& =E\left[Y\right\{1,M\left(x\right)\}-Y\{0,M\left(x\right)\left\}\right]=\beta \\ TE& =E\left[Y\right\{1,M\left(1\right)\}-Y\{0,M\left(0\right)\left\}\right]=\beta +\alpha \gamma \end{array}$$

Model assumptions

There are three main assumptions for this quantity to be a valid estimator of the causal mediation effect

• the effect of treatment is linear.
• there is no interaction between mediator $M$ and treatment $X$.
• the sequential ignorability assumption holds.

Sobel's test

Based on estimators of coefficients $\hat{\alpha }$ and $\hat{\gamma }$, construct a test statistic $$S=\frac{\hat{\alpha }\hat{\gamma }-0}{se\left(\hat{\alpha }\hat{\gamma }\right)}$$

The coefficient and variance estimates can be extracted from the output of the regression model.

In large sample, $S\stackrel{\cdot }{\sim }Normal(0,1)$, but this approximation may be poor in small samples.

Other test statistics

Sobel's test is not the only test. Alternative statistics are discussed in

MacKinnon, D. P., Lockwood, C. M., Hoffman, J. M., West, S. G., & Sheets, V. (2002). A comparison of methods to test mediation and other intervening variable effects. Psychological Methods, 7(1), 83–104. https://doi.org/10.1037/1082-989X.7.1.83

Alternative

An alternative to estimate p-value and the confidence interval is through the nonparametric bootstrap with the percentile method, popularized by Preacher and Hayes (2004)

Nonparametric bootstrap: repeat $B$ times, say $B=10000$

1. sample $n$ (same as original number of observations) tuples $(Y_i,X_i,M_i)$ from the database with replacement to obtain a new sample.
2. recalculate estimates ${\hat{\alpha }}^{\left(b\right)}{\hat{\gamma }}^{\left(b\right)}$ for each bootstrap dataset

Bootstrap confidence intervals

Percentile-based method: for a equitailed $1-\alpha$ interval

1. Run the nonparametric bootstrap and obtain estimates ${\hat{\alpha }}^{\left(b\right)}$ and ${\hat{\gamma }}^{\left(b\right)}$ from the $b$th bootstrap sample.

2. Compute the $\alpha /2$ and $1-\alpha /2$ empirical quantiles of $$\{{\hat{\alpha }}^{\left(b\right)}{\hat{\gamma }}^{\left(b\right)}{\}}_{b=1}^B.$$

Boostrap two-sided p-value

Compute the sample proportion of bootstrap statistics that are larger/smaller than zero.

1. Order bootstrap statistics $S^{\left(1\right)}\le \cdots \le S^{\left(B\right)}$ and let $S^{\left(0\right)}=-\infty$, $S^{(M+1)}=\infty$.
2. Find $M$ ( $0\le M\le B$ ) such that $S^{\left(M\right)}<0\le S^{(M+1)}$ (if it exists)
3. The $p$-value is

$$p=2min\{M/B,1-M/B\}.$$

Model assumptions

Same assumptions as analysis of variance and linear models

• Linearity of the mean model
  • check via residual plots, fitted values $\hat{y}$ against $m$ and $x$
• Independent/uncorrelated errors
  • no confounding
• Equal variance of errors in each model (homoskedasticity)
• Large samples

Causal assumptions

Conclusions about mediation are valid only when causal assumptions hold.

Assuming that $X$ is randomized, we need

• Lack of interaction between $X$ and $M$ (moderated mediation)
• Causal direction: $M\to Y$
  • $M$ must be an antecedent, i.e., must be measured before $Y$
• Reliability of $M$ (no measurement error)
• No confounding between $Y$ and $M$
• Effect constant over individuals/levels

Sensitivity analysis

The no-unmeasured confounders assumption should be challenged.

Check the robustness of the conclusions by considering potential correlation between errors, as $$E\left(\hat{\gamma }\right)=\gamma +Cor({\epsilon }_m,{\epsilon }_y)\sqrt{\frac{Va\left({\epsilon }_y\right)}{Va\left({\epsilon }_m\right)}}$$

• We vary $\rho =Cor({\epsilon }_m,{\epsilon }_y)$ to assess the sensitivity to confounding.
• The medsens function in the R package mediation implements the diagnostic of Imai, Keele and Yamamoto (2010) for the linear mediation model.

Defaults of linear mediation models

Extension: moderated mediation

Consider a more complex setting where the effect of the experimental factor $X$ depends on the mediator, a case termed moderated mediator Judd and Kenny (1982).

In this case, the equation for the response variable becomes $$\begin{array}{c}E(Y\mid M=m,X=x,Z=z)=c_Y+\beta x+\gamma m+\kappa xm+z\omega \end{array}$$

ACME for moderated mediation

Upon substituting the equations for both inside the definition of average causal mediation effect, we find that the latter equals $$\begin{array}{c}ACME\left(x\right)=(\gamma +\kappa x)\left\{M\right(1)-M(0\left)\right\}=\alpha (\gamma +\kappa x).\end{array}$$ and thus the value differs depending on experimental regime (treatment or control), due to the presence of the interaction.

Both the average direct and total effects now depend on the theoretical average values of the covariates $Z$ added to the model to control for confounding.

General approach

Imai et al. (2010) suggest using simulation for general models that naturally account for nonlinear effects, different natures of the mediator (binary, categorical, etc.) and the response.

General approach

Key references